/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 4846304

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile jest liczb pięciocyfrowych, które mają trzy cyfry parzyste i dwie nieparzyste?

Rozwiązanie

Sposób I

Pomyślmy na ile sposobów można napisać 5 cyfr tak, aby otrzymać liczbę opisaną w treści zadania. Musimy najpierw ustalić miejsca dla cyfr nieparzystych (miejsca cyfr parzystych są wtedy jednoznacznie wyznaczone). Możemy to zrobić na

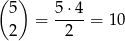
( ) 5 5-⋅4 2 = 2 = 1 0

sposobów.

Jeżeli już jest ustalone, gdzie stoją cyfry parzyste, a gdzie nieparzyste, to każdą cyfrę możemy wybrać na 5 sposobów. Prawda? Nie całkiem, bo na początku nie może stać 0. Aby poradzić sobie z tym problemem osobno zajmijmy się przypadkiem gdy pierwsza cyfra jest nieparzysta – są 4 takie układy cyfr (drugą cyfrę nieparzystą możemy rozmieścić na 4 sposoby). W takiej sytuacji rzeczywiście każdą cyfrę możemy wybrać na 5 sposobów, więc jest

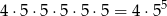
4⋅5 ⋅5 ⋅5⋅ 5⋅5 = 4⋅55

liczb tej postaci.

Teraz przypadek, gdy na początku jest cyfra parzysta – jest 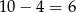10− 4 = 6 takich układów. W takiej sytuacji pierwszą cyfrę możemy wybrać na 4 sposoby (nie może być 0), a wszystkie pozostałe na 5 sposobów. Jest więc

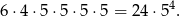
6⋅4 ⋅5 ⋅5⋅ 5⋅5 = 24⋅ 54.

liczb tej postaci.

W sumie jest więc

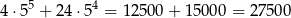
4 ⋅55 + 24⋅ 54 = 12500 + 15 000 = 275 00

liczb spełniających warunki zadania.

Sposób II

Jeżeli pierwszą cyfrą utworzonej liczby jest liczba parzysta, to możemy ją wybrać na 4 sposoby. Wśród pozostałych cyfr mają być dwie cyfry nieparzyste – ich miejsce możemy wybrać na

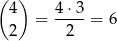
( ) 4 4⋅-3 2 = 2 = 6

sposobów. Gdy już to ustalimy, każdą z pozostałych 4 cyfr możemy wybrać na 5 sposobów. W sumie jest więc

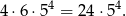
4 4 4 ⋅6 ⋅5 = 24 ⋅5 .

takich liczb.

Jeżeli natomiast pierwsza cyfra jest nieparzysta, to możemy ją wybrać na 5 sposobów. Potem musimy jeszcze ustalić, gdzie ma być druga cyfra nieparzysta – możemy to zrobić na 4 sposoby. Gdy już to ustalimy, każdą z pozostałych 4 cyfr możemy wybrać na 5 sposobów. W sumie jest więc

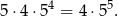
5⋅ 4⋅5 4 = 4⋅5 5.

takich liczb.

Wszystkich liczb spełniających warunki zadania jest więc

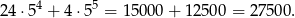
24⋅ 54 + 4⋅55 = 15000 + 1250 0 = 27500 .

 
Odpowiedź: 27 500

Wersja PDF