/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 5246249

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile jest liczb naturalnych pięciocyfrowych, których zapis dziesiętny składa się z trzech różnych cyfr?

Rozwiązanie

Ponieważ liczba ma być 5 cyfrowa, mamy dwie możliwości: albo jedna z cyfr występuje 3 razy, albo dwie z cyfr powtarzają się po 2 razy.

Zajmijmy się najpierw pierwszą sytuacją. Miejsca dla trzech powtarzających się cyfr możemy wybrać na

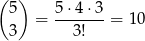
( ) 5 5⋅-4⋅3- 3 = 3! = 10

sposobów. Teraz pierwszą cyfrę (najbardziej znaczącą) liczby możemy wybrać na 9 sposobów (nie może być 0), kolejną różną cyfrę też możemy wybrać na 9 sposobów (musi być różna od już wybranej cyfry), a ostatnią możemy wybrać na 8 sposobów. W sumie jest więc w tym przypadku

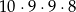
10⋅ 9⋅9 ⋅8

liczb spełniających warunki zadania.

W drugiej sytuacji liczymy następująco: na 5 sposobów możemy wybrać miejsce dla pojedynczej cyfry, potem pozostałe 4 miejsca możemy na 3 sposoby podzielić na dwie grupy po dwie cyfry (według jednego ze schematów: 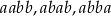aabb ,abab,abba ). Gdy już ustalone są miejsca podwójnych cyfr, tak jak poprzednio, pierwszą cyfrę wybieramy na 9 sposobów, druga różną cyfrę też na 9 sposobów i ostatnią na 8 sposobów. W sumie jest więc w tym przypadku

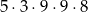
5⋅ 3⋅9 ⋅9 ⋅8

liczb.

Razem jest więc

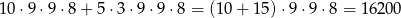
1 0⋅9 ⋅9 ⋅8+ 5⋅3 ⋅9 ⋅9 ⋅8 = (10 + 15) ⋅9 ⋅9⋅8 = 16200

liczb spełniających warunki zadania.  
Odpowiedź: 16200

Wersja PDF