Zadanie nr 5410484
Karol do szyfrowania swoich danych postanowił używać pięciocyfrowych liczb naturalnych 
, które mają co najmniej jedną z dwóch cech: w zapisie dziesiętnym liczby 
występuje przynajmniej jedna z cyfr: 3, 4, 5, 6, 7, 8, 9, lub liczba 
nie jest podzielna przez 3. Ile jest takich liczb pięciocyfrowych?
Rozwiązanie
Liczby, które nie są podzielne przez 3 łatwo policzyć, ale z liczbami, które zawierają jedną z cyfr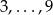 
jest dużo większy problem. Dlatego spróbujmy się zastanowić jakie liczby pięciocyfrowe nie spełniają warunków zadania? Są to dokładnie liczby, które można zapisać przy pomocy cyfr 0, 1, 2, i które dzielą się przez 3. Obliczmy ile ich jest.
Cyfry takiej liczby muszą być równe (na razie nie zwracamy uwagi na ich kolejność):
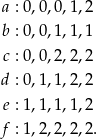
Obliczymy kolejno, ile jest możliwości utworzenia liczb o takich cyfrach. Najprostsze są przypadki 
i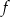 
– w każdym z nich jest 5 możliwości ustawienia jednej wyróżnionej cyfry. W przypadkach 
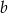i 
na początku musimy umieścić niezerową cyfrę i potem mamy
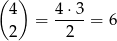
możliwości umieszczenia dwóch zer. W przypadku 
na początku umieszczamy 1 lub 2 i potem mamy 4 możliwości umieszczenia drugiej niezerowej cyfry, więc jest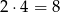 
liczb tego typu. Pozostał przypadek 
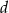– zajmijmy się najpierw liczbami, które zaczynają się od jedynki. Wtedy na
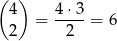
sposobów umieszczamy dwójki i na dwa sposoby możemy umieścić pozostałe dwie cyfry. Jest więc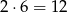 
liczb typu 
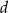zaczynających się od jedynki. Oczywiście tyle samo liczb zaczyna się od dwójki. W sumie są więc
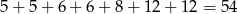
liczby pięciocyfrowe, które nie spełniają warunków zadania. Wszystkich liczb pięciocyfrowych jest
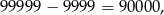
więc jest
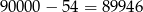
liczb spełniających warunki zadania.
Odpowiedź: 89946
