Zadanie nr 5488861
Rozpatrujemy wszystkie liczby naturalne dziesięciocyfrowe, w zapisie których mogą występować wyłącznie cyfry 1, 2, 3, przy czym cyfra 1 występuje dokładnie trzy razy. Uzasadnij, że takich liczb jest 15 360.
Rozwiązanie
Liczymy, na ile sposobów można utworzyć liczbę o własnościach opisanych w treści zadania. Miejsca dla cyfry 1 można wybrać na
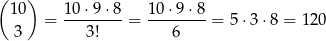
sposobów. Na pozostałych 7 miejscach dowolnie wpisujemy jedną z pozostałych dwóch cyfr, więc sumie jest
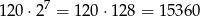
możliwości.

