Zadanie nr 5834060
Rozważamy wszystkie liczby naturalne pięciocyfrowe zapisane przy użyciu cyfr 1, 3, 5, 7, 9, bez powtarzania jakiejkolwiek cyfry. Oblicz sumę wszystkich takich liczb.
Rozwiązanie
Zauważmy najpierw, że suma jedności wszystkich takich liczb będzie równa
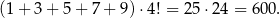
Tak jest bo każda z cyfr pojawi się dokładnie w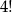 
liczb jako cyfra jedności.
Analogicznie, suma wszystkich dziesiątek utworzonych liczb będzie równa
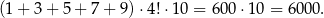
I tak dalej dla kolejnych cyfr. Interesująca nas suma jest więc równa
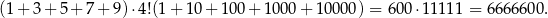
Odpowiedź: 6666600
