Zadanie nr 6104994

Zauważmy po pierwsze, że z treści zadania wynika, że wśród cyfr tworzonej liczby nie ma również cyfr: 9 i 7. Brak 9–ki jest oczywisty, a brak 7–ki wynika z braku 1–ki. Ponadto, jest tylko jedna liczba z cyfrą 8:

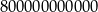
Pozostało nam zatem 5 cyfr: 0, 2, 3, 5, 6.

Jeżeli w utworzonej liczbie jest 6–stka, to jest jeszcze jedna niezerowa cyfra i jest nią 2–ka. Oczywiście jedna z tych cyfr musi być umieszczona jako pierwsza (najbardziej znacząca), a drugą możemy umieścić na 11 sposobów. Są więc

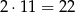
takie liczby (mnożymy przez 2, bo przy ustalonych miejscach niezerowych cyfr możemy te cyfry umieścić na 2 sposoby).

Zauważmy, że identyczna sytuacja ma miejsce, gdy jedną z cyfr tworzonej liczby jest 5–ka. Wtedy jest jeszcze jedna niezerowa cyfra i jest nią 3–ka. Jak wyżej, są

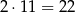
takie liczby.

Jeżeli jedną z cyfr w utworzonej liczbie jest 3–ka i nie ma 5–ki, to 3–ki muszą być dwie i oprócz tego musi być jeszcze jedna 2–ka. Jeżeli dwójka jest pierwszą cyfrą, to trójki możemy umieścić na

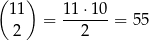
sposobów. Jeżeli natomiast na pierwszym miejscu jest 3–ka, to pozostałe dwie niezerowe cyfry możemy umieścić na

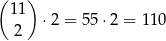
sposobów (wybieramy miejsca dla tych dwóch niezerowych cyfr, a potem umieszczamy te cyfry).

Pozostała zatem sytuacja, gdy w liczbie mamy cztery dwójki i resztę zer. Oczywiście jedna dwójka musi być na początku, a pozostałe 3 możemy umieścić na

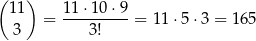
sposobów.

W sumie jest więc

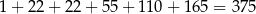
liczb spełniających warunki zadania.  
Odpowiedź: 375