Zadanie nr 6517455

Obliczmy najpierw ile jest liczb, w których pierwsza cyfra nie jest ani 3-ką ani 5-ką. Miejsca dla 3-ek możemy wybrać na

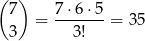
sposobów (3-ki nie mogą być ani na początku, ani na końcu). Gdy już ustaliliśmy, gdzie są 3-ki, to 5-ki możemy umieścić na

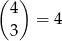
sposoby. Gdy już są ustalone miejsca dla 3-ek i 5-ek, wybieramy pierwszą cyfrę na 7 sposobów (nie może być 0, 3 ani 5), ostatnią na 5 sposobów (musi być parzysta) i ostatnią wolną cyfrę na 8 sposobów (nie może być równa ani 3, ani 5). W sumie jest więc w tym przypadku

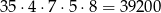
możliwości.

Jeżeli natomiast na pierwszym miejscu jest np. 3-ka, to najpierw wybieramy miejsca dla 5-ek, możemy to zrobić na

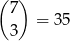
sposobów. Potem wybieramy miejsca dla pozostałych dwóch 3-ek, możemy to zrobić na

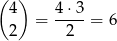
sposobów. Na koniec wybieramy cyfrę jedności na 5 sposobów i każdą z ostatnich dwóch wolnych cyfr na 8 sposobów (nie mogą być równe ani 3, ani 5). W sumie jest więc w tym przypadku

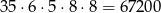
liczb.

Liczb z 5-ką na początku jest dokładnie tyle samo, ile liczb z 3-ką na początku (bo 3 i 5 pełnią dokładnie taką samą rolę), więc w sumie jest

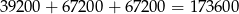
liczb spełniających warunki zadania.  
Odpowiedź: 173600