/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 6734909

Dodaj do ulubionych
Dodaj do rozwiązanych

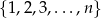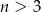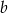Ze zbioru {1,2,3,...,n} , gdzie n > 3 losujemy bez zwracania dwie liczby. Oznaczmy je, w kolejności losowania przez a i b . Ile jest możliwości wylosowania:

  • dowolnej pary liczb?
  • pary liczb, dla której a > b − 1 ?
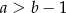  • pary liczb, dla której |a− b| > 2 ?

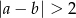Rozwiązanie

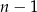  • Pierwszą liczbę możemy wybrać na n sposobów, a drugą na n − 1 sposobów. Jest więc 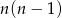n (n− 1) możliwości.  
    Odpowiedź: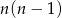 n(n − 1)
  • Podany warunek oznacza, że 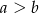a > b (bo liczby mają być różne). Par o tej własności jest dokładnie połowa (każdej takiej parze odpowiada dokładnie jedna para spełniająca 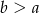b > a – wystarczy zamienić kolejność liczb). Jest więc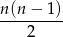
    n (n− 1) --------- 2

    takich par.  
    Odpowiedź: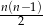 n(n−1) 2

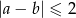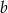  • O wiele łatwiej jest policzyć pary, które nie spełniają podanego warunku, czyli spełniające |a − b| ≤ 2 . Warunek ten oznacza, że liczby a i b są od siebie odległe o 1 lub 2.

    Wypiszmy takie pary:

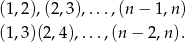
    (1,2),(2,3),...,(n − 1,n) (1,3)(2,4),...,(n − 2,n ).

    Ponieważ ważna jest dla nas kolejność wylosowanych liczb, możliwości jest dwa razy więcej niż wypisanych par, czyli

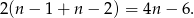
    2(n − 1+ n − 2) = 4n − 6.

    Teraz pora sobie przypomnieć, że liczyliśmy złe pary. Dobrych jest

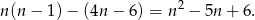
    n(n − 1)− (4n − 6) = n2 − 5n + 6.

     
    Odpowiedź: 2 n − 5n + 6

Wersja PDF