Zadanie nr 6974643
Oblicz, ile jest stucyfrowych liczb naturalnych o sumie cyfr równej 4.
Rozwiązanie
Zastanówmy się jaka może być największa cyfra liczby stucyfrowej o sumie cyfr równej 4?
Oczywiście żadna cyfra nie może być większa od 4 i jeżeli jedną z cyfr jest 4, to wszystkie pozostałe cyfry muszą być zerami. Jest tylko jedna taka liczba: 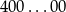 .
.
Jeżeli największą cyfrą jest 3, to musi być jeszcze jedna jedynka i reszta to same zera. Policzmy ile jest takich liczb. Pierwszą cyfrę możemy wybrać na dwa sposoby (może to być 3 lub 1), a drugą niezerową cyfrę możemy umieścić na jednej z 99 pozostałych pozycji. Jest więc
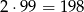
takich liczb.
Jeżeli największą cyfrą jest 2, to mamy dwie możliwości: albo są dwie dwójki, albo jedna dwójka i dwie jedynki. Jest 99 liczb z dwoma dwójkami (pierwsza musi stać na początku, a druga na jednym z pozostałych 99 miejsc). Obliczmy, ile jest liczb z jedną dwójką i dwoma jedynkami. Jeżeli dwójka jest na początku, to pozostałe dwie jedynki możemy umieścić na
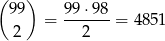
sposobów, jest więc 4851 takich liczb. Jeżeli na początku jest jedynka, to możliwych liczb jest
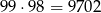
(wybieramy miejsce dla jedynki i potem dla dwójki).
Ostatnia możliwość to liczby składające się z czterech jedynek i 96 zer. Jedna jedynka musi być pierwszą cyfrą, a pozostałe 3 możemy umieścić na
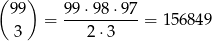
sposobów.
W sumie jest więc
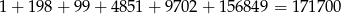
liczb spełniających warunki zadania.
Odpowiedź: 171700

