Zadanie nr 7055337
Ze zbioru liczb 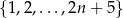 wybieramy jednocześnie dwie liczby (nie uwzględniamy kolejności). Na ile sposobów możemy to zrobić, tak aby otrzymać dwie liczby takie, że:
wybieramy jednocześnie dwie liczby (nie uwzględniamy kolejności). Na ile sposobów możemy to zrobić, tak aby otrzymać dwie liczby takie, że:
- ich różnica będzie liczbą parzystą,
- suma ich kwadratów będzie liczbą podzielną przez cztery?
Rozwiązanie
- Aby różnica była liczbą parzystą to obie liczby muszą być parzyste bądź nieparzyste. Liczby nieparzyste w podanym przedziale to
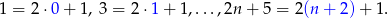
Jest zatem tych liczb
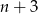 . Podobnie, liczb parzystych jest
. Podobnie, liczb parzystych jest 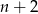 . Mamy więc
. Mamy więc 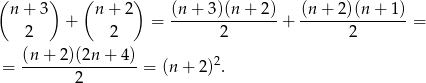
takich par.
Odpowiedź: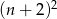
- Kiedy suma kwadratów dwóch liczb jest podzielna przez 4? Na pewno muszą być tej samej parzystości. Jeżeli obie są nieparzyste, czyli np.
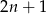 i
i 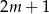 , to
, to 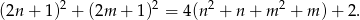
A więc liczba ta nie dzieli się przez 4. Zatem obie liczby muszą być parzyste. Z poprzedniego podpunktu wiemy, że jest
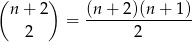
takich par.
Odpowiedź: