/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 7146397

Dodaj do ulubionych
Dodaj do rozwiązanych

Z cyfr 1,2,3,4,5,6,7,8 tworzymy liczby sześciocyfrowe. Ile można utworzyć takich liczb w których cyfra 1 występuje co najmniej trzy razy, a pozostałe cyfry są różne między sobą?

Rozwiązanie

Będziemy liczyć takie liczby, w zależności od ilości jedynek w ich zapisie.

Jest jedna liczba z 6 jedynkami.

Jeżeli jest 5 jedynek, to na 6 sposobów możemy wybrać miejsce 6 cyfry, i na 7 sposobów jaka to będzie cyfra. Są więc 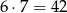6⋅7 = 42 takie liczby.

Jeżeli są 4 jedynki, to na

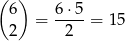
( 6) 6 ⋅5 = ---- = 1 5 2 2

sposobów wybieramy, gdzie będą inne cyfry. Same cyfry możemy wybrać na 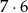7 ⋅6 sposobów. Daje to nam

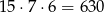
15⋅ 7⋅6 = 630

takich liczb.

Pozostały nam liczby z 3 jedynkami. Miejsca pozostałych cyfr możemy wybrać na

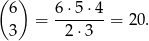
( ) 6 6⋅5 ⋅4 3 = -2⋅-3--= 20.

Te dodatkowe cyfry wybieramy na 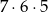7⋅6 ⋅5 sposobów. Jest więc

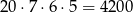
20 ⋅7⋅6 ⋅5 = 4200

takich liczb.

W sumie mamy

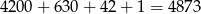
420 0+ 630+ 42 + 1 = 487 3

takich liczb.  
Odpowiedź: 4873

Wersja PDF