Zadanie nr 8182229
Ile jest liczb pięciocyfrowych, spełniających jednocześnie następujące cztery warunki:
(1) cyfry setek, dziesiątek i jedności są parzyste,
(2) cyfra setek jest większa od cyfry dziesiątek,
(3) cyfra dziesiątek jest większa od cyfry jedności,
(4) w zapisie tej liczby nie występuje cyfra 9.
Rozwiązanie
Sposób I
Zauważmy, że na pierwsze dwie cyfry utworzonej liczby mamy bardzo małe ograniczenia – dotyczy ich jedynie warunek (4). Zajmijmy się więc trudniejszą częścią tej liczby, czyli trzema najmniej znaczącymi cyframi. Wypiszmy wszystkie możliwe konfiguracje trzech ostatnich cyfr.
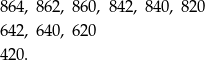
Do każdej z tych końcówek możemy dobrać drugą cyfrę na 9 sposobów (może być 0, ale nie może być 9), oraz pierwszą cyfrę na 8 sposobów (nie może być 0 i nie może być 9). Wszystkich możliwości jest więc
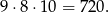
Sposób II
Tak jak w poprzednim sposobie, policzmy najpierw na ile sposobów możemy wybrać trzy ostatnie cyfry. Zauważmy, że muszą to być 3 różne cyfry parzyste – takie trzy liczby można wybrać na
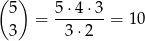
sposobów. Zauważmy, że jeżeli ustalimy już jakie trzy liczby parzyste to ich kolejność jako cyfr danej liczby jest jednoznacznie ustalona przez warunki (2)–(3).
Pozostało dobrać pierwsze dwie cyfry – liczymy dokładnie tak samo jak w I sposobie.
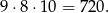
Odpowiedź: 720

