Zadanie nr 8349257
Oblicz, ile jest siedmiocyfrowych liczb naturalnych takich, że iloczyn wszystkich ich cyfr w zapisie dziesiętnym jest równy 28.
Rozwiązanie
Sprawdźmy najpierw w jaki sposób możemy 28 napisać jako iloczyn cyfr.
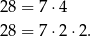
Mamy zatem dwie różne sytuacje.
Obliczmy ile jest liczb, których cyfry to 7, 4 i pięć jedynek. Miejsce dla 7–ki możemy wybrać na 7 sposobów, dla 4–ki na 6 sposobów, a na pozostałych miejscach umieszczamy 1–ki. Są więc
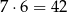
liczby tej postaci.
Pozostało obliczyć ile jest liczb, których cyfry to 2, 2, 7 i cztery jedynki. Miejsca dla dwójek możemy wybrać na
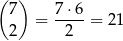
sposobów. Do tego wybieramy na 5 sposobów miejsce dla siódemki, a na pozostałych miejscach wpisujemy jedynki. Jest więc
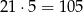
liczb tej postaci.
W sumie jest więc
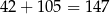
liczb spełniających warunki zadania.
Odpowiedź: 147

