/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 8654156

Oblicz, ile jest liczb sześciocyfrowych, w których zapisie nie występuje zero, natomiast występują dwie dziewiątki, jedna szóstka i suma wszystkich cyfr jest równa 30.

Wersja PDF

Rozwiązanie

Miejsce dla szóstki możemy wybrać 6 sposobów. Gdy to zrobimy, to miejsca dla dziewiątek możemy wybrać na

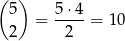
( ) 5 = 5-⋅4 = 1 0 2 2

sposobów. Suma pozostałych 3 cyfr musi być równa

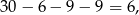
3 0− 6− 9 − 9 = 6,

więc te cyfry mogą być równe 1, 1, 4, lub 1, 2, 3 lub wreszcie 2, 2, 2. W pierwszym przypadku są 3 możliwości umieszczenia tych cyfr (na trzy sposoby możemy umieścić 4, a na dwóch pozostałych miejscach umieszczamy 1). W drugim przypadku możliwości umieszczenia tych cyfr jest

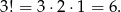
3! = 3⋅2 ⋅1 = 6.

W trzecim przypadku jest tylko jedna możliwość.

W sumie jest więc

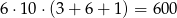
6⋅ 10⋅(3 + 6 + 1) = 600

liczb spełniających warunki zadania.  
Odpowiedź: 600

Wersja PDF