/Szkoła średnia/Kombinatoryka/Zbiory liczb

Zadanie nr 8748752

Ze zbioru 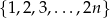{1,2,3,...,2n } , gdzie 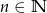n ∈ N , losujemy jednocześnie trzy liczby. Ile mamy możliwości wylosowania takich trzech liczb, których suma jest nieparzysta?

Wersja PDF

Rozwiązanie

Skoro suma wylosowanych liczb ma być nieparzysta to albo wszystkie trzy są nieparzyste, albo jest jedna nieparzysta i dwie parzyste.

Dokładnie połowa danych liczb jest nieparzysta, więc 3 nieparzyste możemy wybrać na

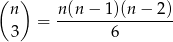
( ) n n(n-−-1-)(n−--2) 3 = 6

sposobów.

Dwie liczby parzyste możemy wybrać na

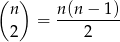
(n ) n(n − 1) = --------- 2 2

sposobów. Do tego możemy dobrać trzecią (nieparzystą) liczbę na n sposobów. Daje nam to w sumie

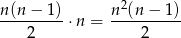
2 n(n-−-1)- n-(n-−-1)- 2 ⋅n = 2

trójek z dokładnie dwoma parzystymi liczbami.

Razem mamy

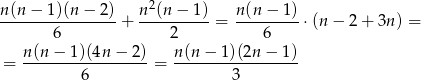
n (n− 1)(n − 2) n 2(n− 1) n (n − 1) ---------------- + ---------- = --------- ⋅(n − 2 + 3n) = 6 2 6 n-(n-−-1)(4n-−-2) n(n-−-1-)(2n−--1) = 6 = 3

możliwości.  
Odpowiedź: n(n− 1)(2n−1) ------3-----

Wersja PDF