Zadanie nr 9240154
Oblicz, ile jest liczb naturalnych pięciocyfrowych, których suma cyfr jest równa 5?
Rozwiązanie
Wypiszmy na ile sposobów 5 może być sumą niezerowych cyfr.
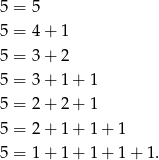
Pierwszemu i ostatniemu rozkładowi odpowiadają liczby 50000 i 11111. Łatwo jest też obliczyć, ile jest liczb odpowiadających przedostatniemu rozkładowi: na 4 sposoby wybieramy miejsce dla 0 (nie może być na początku), potem na 4 sposoby miejsce dla 2, a na pozostałych miejscach umieszczamy 1–ki. W sumie jest więc 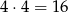 takich liczb.
takich liczb.
Obliczmy teraz, ile jest liczb odpowiadających rozkładowi 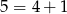 . Na pierwszym miejscu możemy umieścić 4 lub 1, a drugą cyfrę niezerową możemy umieścić na jednym z pozostałych 4 miejsc. Wszystkie pozostałe cyfry to zera. Jest więc
. Na pierwszym miejscu możemy umieścić 4 lub 1, a drugą cyfrę niezerową możemy umieścić na jednym z pozostałych 4 miejsc. Wszystkie pozostałe cyfry to zera. Jest więc 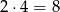 takich liczb. Zauważmy, że dokładnie ten sam rachunek możemy zastosować w przypadku liczb odpowiadających rozkładowi
takich liczb. Zauważmy, że dokładnie ten sam rachunek możemy zastosować w przypadku liczb odpowiadających rozkładowi 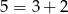 .
.
Pozostały jeszcze rozkłady 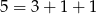 i
i 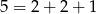 . W obu przypadkach będzie działał dokładnie ten sam rachunek, więc skoncentrujmy się na
. W obu przypadkach będzie działał dokładnie ten sam rachunek, więc skoncentrujmy się na 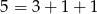 . Miejsca dla zer możemy wybrać na
. Miejsca dla zer możemy wybrać na
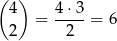
sposobów (zero nie może być na początku). Na jednym z pozostałych 3 miejsc umieszczamy 3, a na dwóch pozostałych 1–ki. W sumie jest więc
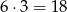
takich liczb. Dokładnie tyle samo jest liczb odpowiadających rozkładowi 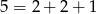 .
.
W sumie jest więc
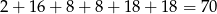
liczb spełniających warunki zadania.
Odpowiedź: 70

