Zadanie nr 9353698
Spośród liczb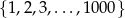 
losujemy jednocześnie dwie, które oznaczamy 
i 
. I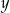le jest możliwości wylosowania takiej pary liczb 
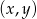, dla której:
jest podzielne przez 23, a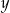 
nie jest podzielne przez 23? 
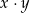jest podzielne przez 23?
Rozwiązanie
Wypiszmy liczby w danym przedziale, które są podzielne przez 23:
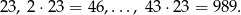
Są więc 43 takie liczby.
- Liczbę
można wybrać na 43 sposoby, a liczbę 
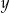na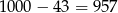 
. Jest więc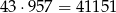 
możliwości.
Odpowiedź: 41151 - Aby iloczyn był podzielny przez 23, jedna z liczb musi się dzielić przez 23. Osobno policzmy sytuacje, gdy tylko pierwsza, tylko druga lub obie dzielą się przez 23. Pierwsze dwie sytuacje liczyliśmy wyżej, a sytuacji z obiema liczbami podzielnymi przez 23 jest
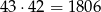(bo liczby mają być różne). W sumie mamy więc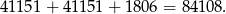 
Odpowiedź: 84108
