Zadanie nr 9650024
Oblicz ile liczb podzielnych przez 7 znajduje się w przedziale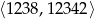 
.
Rozwiązanie
Sposób I
Sprawdzamy, czy 1238 dzieli się przez 7. Nie dzieli się, ale iloraz to trochę ponad 176, zatem pierwszą liczbą podzielną przez 7 w tym przedziale będzie
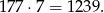
Podobnie sprawdzamy przy prawym końcu przedziału i otrzymujemy największą liczbę podzielną przez 7, która jest w tym zbiorze:
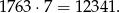
Zatem liczb podzielnych przez 7 jest tyle, ile liczb naturalnych pomiędzy 177 i 1763, czyli
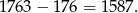
Sposób II
Interesujące nas liczby tworzą ciąg arytmetyczny o różnicy 7 i jak poprzednio ustalamy, że pierwszym jego wyrazem jest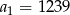 
, a ostatnim 
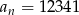. Ze wzoru na 
-ty wyraz ciągu arytmetycznego wyliczymy 
.
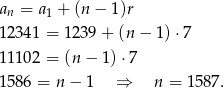
Odpowiedź: 1587
