Zadanie nr 9651832
Rozważamy wszystkie liczby naturalne pięciocyfrowe zapisane przy użyciu cyfr 0, 3, 5, 7, 9, bez powtarzania jakiejkolwiek cyfry. Oblicz sumę wszystkich takich liczb.
Rozwiązanie
Zastanówmy się na początek nad cyframi jedności. Zero jest cyfrą jedności w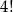 
liczb (możemy dowolnie ustalić kolejność pierwszych czterech cyfr). Każda z pozostałych cyfr jest natomiast cyfrą jedności w
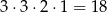
liczbach (najbardziej znacząca cyfra nie może być zerem, więc możemy ją wybrać na 3 sposoby, a kolejność pozostałych 3 cyfr ustalamy dowolnie). To oznacza, że suma jedności wszystkich takich liczb będzie równa
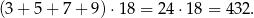
Analogicznie, suma wszystkich dziesiątek utworzonych liczb będzie równa
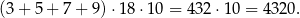
I tak dalej – taki sam rachunek mamy dla cyfr setek i cyfr tysięcy.
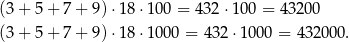
Przy cyfrach dziesiątek tysięcy musimy być jednak bardziej ostrożni. Każda z niezerowych cyfr może się tam pojawić na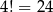 
sposoby (pozostałe cyfry umieszczamy w dowolnej kolejności). Więc suma cyfr dziesiątek tysięcy jest równa
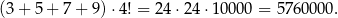
Interesująca nas suma jest więc równa
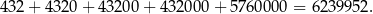
Odpowiedź: 6239952
