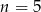Zadanie nr 6545747
Rozwiąż równanie 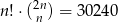 .
.
Rozwiązanie
Przekształcamy dane równanie
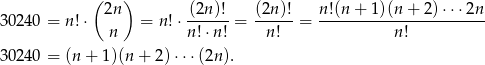
Zauważmy teraz, że prawa strona jest rosnącą funkcją  (tzn. zwiększa się jeżeli zwiększamy
(tzn. zwiększa się jeżeli zwiększamy  ), więc powyższe równanie może mieć tylko jedno rozwiązanie. Próbujemy znaleźć to rozwiązanie podstawiając kolejno
), więc powyższe równanie może mieć tylko jedno rozwiązanie. Próbujemy znaleźć to rozwiązanie podstawiając kolejno 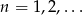 . Gdy to zrobimy, okaże się, że równanie jest spełnione dla
. Gdy to zrobimy, okaże się, że równanie jest spełnione dla 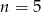 :
:
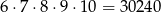
Odpowiedź: