Zadanie nr 8355749
Z liter 26 literowego alfabetu łacińskiego tworzymy czteroliterowe kody, przy czym każdy kod składa się z czterech różnych liter, które zostały wybrane z pewnych 6 kolejnych liter alfabetu. Ile jest takich kodów?
Rozwiązanie
Nie jest to konieczne, ale dla lepszej orientacji wypiszmy litery alfabetu łacińskiego:
Zauważmy, że jeżeli ustalimy litery z jakich ma składać się kod, to możemy ustalić ich kolejność w kodzie na
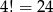
sposoby. Wystarczy zatem obliczyć, ile jest kodów z literami uporządkowanymi rosnąco (w sensie kolejności w alfabecie), a na koniec przemnożymy otrzymany wynik przez 24.
Sposób I
Zastanówmy się jaka może być najmniejsza (w sensie kolejności w alfabecie) litera w utworzonym kodzie. Jeżeli jest to 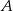 , to pozostałe trzy litery wybieramy spośród następnych 5 liter, więc możemy to zrobić na
, to pozostałe trzy litery wybieramy spośród następnych 5 liter, więc możemy to zrobić na
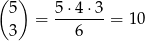
sposobów. Dokładnie tyle samo jest kodów zaczynających się od 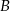 , tyle samo zaczynających się od
, tyle samo zaczynających się od 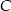 i tak dalej, aż do
i tak dalej, aż do 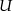 . W sumie jest
. W sumie jest
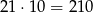
rosnących kodów tego typu.
Pozostały jeszcze dwie możliwości: kod może się zaczynać od 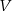 i od
i od 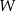 . Jeżeli kod zaczyna się od
. Jeżeli kod zaczyna się od 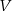 to pozostałe trzy litery wybieramy z następnych 4 liter. Możemy to zrobić na
to pozostałe trzy litery wybieramy z następnych 4 liter. Możemy to zrobić na
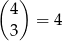
sposoby. Jeżeli wreszcie kod zaczyna się od 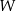 , to jest to kod
, to jest to kod 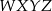 .
.
W sumie jest więc
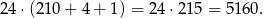
kodów spełniających warunki zadania.
Sposób II
Zastanówmy się jaka może być odległość skrajnych liter w utworzonym kodzie. Jeżeli rosnący kod ma długość 4 (w sensie liczby kolejnych liter, z których został wybrany), to może to być jeden z 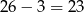 kodów:
kodów:
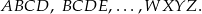
Jeżeli natomiast długość kodu jest równa 5 to na 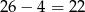 sposoby możemy wybrać jego pierwszą literę, oraz na 3 sposoby możemy wybrać, która ze środkowych liter ma być pominięta, tzn. musi on mieć jedną z postaci
sposoby możemy wybrać jego pierwszą literę, oraz na 3 sposoby możemy wybrać, która ze środkowych liter ma być pominięta, tzn. musi on mieć jedną z postaci
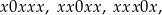
gdzie  symbolizuje literę, którą wybieramy do kodu, a
symbolizuje literę, którą wybieramy do kodu, a 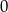 literę, którą pomijamy. Jest więc
literę, którą pomijamy. Jest więc
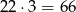
rosnących kodów tego typu.
Jeżeli wreszcie kod ma długość 6, to jego pierwszą literę możemy wybrać na 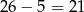 sposobów, oraz na
sposobów, oraz na
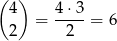
sposobów możemy wybrać, które dwie środkowe litery mają być pominięte. Bardziej wprost, wybieramy jedną z 6 możliwych postaci kodu:
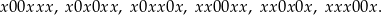
Jest więc
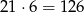
rosnących kodów długości 6.
W sumie jest więc
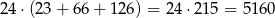
możliwych kodów.
Odpowiedź: 5160

