/Szkoła średnia/Kombinatoryka/Różne

Zadanie nr 8582488

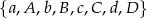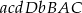Ile jest permutacji zbioru {a,A ,b,B,c,C ,d,D } takich, w których mała litera stoi przed dużą (niekoniecznie obok) np. acdDbBAC ?

Wersja PDF

Rozwiązanie

Sposób I

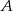Obliczmy na ile sposobów można ustalić kolejność podanych liter tak, aby był spełniony warunek z treści zadania. Miejsce dla liter a i A możemy ustalić na

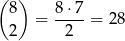
( ) 8 = 8-⋅7 = 2 8 2 2

sposobów. Zauważmy, że po wybraniu tych miejsc nie mamy już żadnego wyboru: literę a umieszczamy po lewej, a 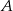A po prawej.

Analogicznie, miejsce dla kolejnych par liter wybieramy odpowiednio na

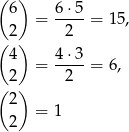
( ) 6 = 6⋅-5 = 15, 2 2 ( 4) 4⋅ 3 = ---- = 6, ( 2) 2 2 2 = 1

sposobów. W sumie jest więc (zasada mnożenia)

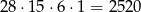
28 ⋅15 ⋅6 ⋅1 = 252 0

możliwości.

Sposób II

Zastanówmy się najpierw ile jest sposobów dobrania dużych liter do układu 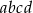abcd tak, aby trzymać ośmioliterowe słowo. Literę 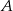A możemy umieścić na 7 sposobów. Gdy to zrobimy, literę 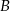B możemy umieścić na 5 sposobów (bo musi być za 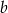b i jedno miejsce zostało już zajęte przez 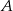A ). Dla litery 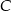C są 3 możliwości, a 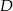D umieszczamy na jednym pozostałym wolnym miejscu. Słowo 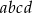abcd możemy więc dokończyć na

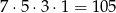
7 ⋅5⋅3 ⋅1 = 105

sposobów. To oczywiście nie koniec, bo teraz na 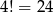4! = 24 sposoby możemy przepermutować litery 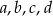a,b,c,d ( i odpowiadające im duże litery). W sumie jest więc

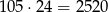
1 05⋅2 4 = 2520

możliwości.  
Odpowiedź: 2520

Wersja PDF