/Szkoła średnia/Geometria

Zadanie nr 1021818

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód trójkąta prostokątnego wynosi 60 cm, a tangens jednego z kątów ostrych jest równy 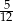512- . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

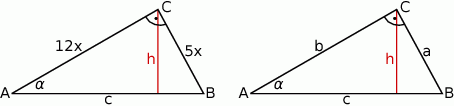
Sposób I

Podany tangens oznacza, że

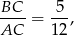
BC--= -5-, AC 12

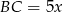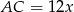więc możemy oznaczyć BC = 5x i AC = 12x dla pewnego x . Na mocy twierdzenia Pitagorasa

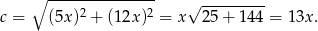
∘ --------------- √ --------- c = (5x)2 + (12x)2 = x 25 + 144 = 13x.

Korzystamy teraz z podanego obwodu.

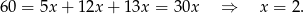
60 = 5x+ 12x + 13x = 30x ⇒ x = 2.

Pole trójkąta jest więc równe

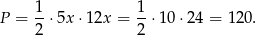
1 1 P = 2-⋅5x ⋅12x = 2-⋅10 ⋅24 = 120.

Wysokość opuszczoną na przeciwprostokątną obliczamy porównując dwa wzory na pole trójkąta.

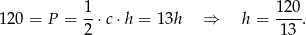
1 120 120 = P = --⋅c ⋅h = 1 3h ⇒ h = ---. 2 13

Sposób II

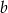Oznaczmy przez a i b długości przyprostokątnych, a przez c długość przeciwprostokątnej trójkąta.

Z podanego tangensa mamy

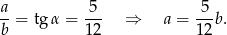
a 5 5 --= tg α = --- ⇒ a = ---b. b 12 1 2

Z podanego obwodu mamy

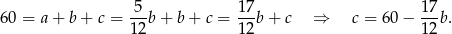
5-- 17- 17- 60 = a+ b+ c = 12b + b + c = 12b + c ⇒ c = 60 − 12b.

Piszemy teraz twierdzenie Pitagorasa.

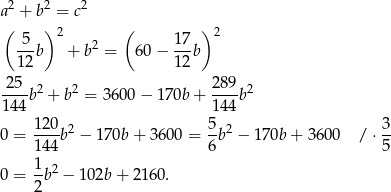
2 2 2 a( + b) = c ( ) 5 2 2 17 2 --b + b = 60− ---b 12 12 -25- 2 2 289- 2 1 44b + b = 36 00− 170b + 144 b 120 5 3 0 = ---b 2 − 17 0b+ 3600 = -b2 − 170b + 360 0 / ⋅-- 144 6 5 0 = 1b2 − 102b + 21 60. 2

Rozwiązujemy teraz otrzymane równanie kwadratowe.

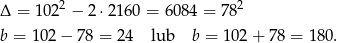
2 2 Δ = 102 − 2⋅ 2160 = 60 84 = 78 b = 102 − 7 8 = 24 lub b = 10 2+ 78 = 180.

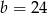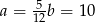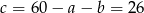Drugie rozwiązanie odpada ze względu na obwód równy 60, więc b = 24 . Stąd 5- a = 12b = 10 i c = 60 − a − b = 26 . Pole trójkąta jest więc równe

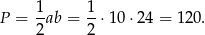
1 1 P = -ab = --⋅10⋅ 24 = 120 . 2 2

Wysokość opuszczoną na przeciwprostokątną obliczamy porównując dwa wzory na pole trójkąta.

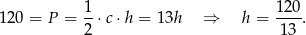
1 120 120 = P = --⋅c ⋅h = 1 3h ⇒ h = ---. 2 13

 
Odpowiedź: 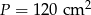2 P = 120 cm , 120- h = 13 cm

Wersja PDF