/Szkoła średnia/Geometria

Zadanie nr 1040340

Dodaj do ulubionych
Dodaj do rozwiązanych

Odległość wierzchołka sześcianu od przekątnej sześcianu (do której dany wierzchołek nie należy) jest równa 4 cm. Oblicz objętość sześcianu.

Rozwiązanie

Zaczynamy od rysunku

PIC

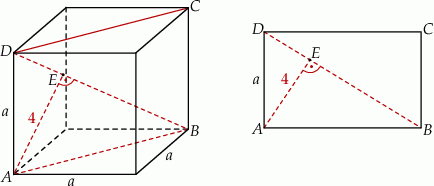
Odcinek 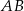AB jest przekątną kwadratu o boku długości a , więc

√ -- AB = a 2.

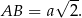
Teraz możemy obliczyć z twierdzenia Pitagorasa długość przekątnej 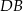DB

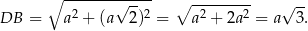
∘ -------√----- ∘ --------- √ -- DB = a2 + (a 2)2 = a2 + 2a2 = a 3.

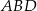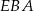Trójkąty ABD i EBA oba są prostokątne i mają jeden wspólny kąt, więc są podobne. Otrzymujemy stąd

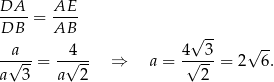
DA-- = AE-- DB AB √ -- a 4 4 3 √ -- -√---= -√--- ⇒ a = -√--- = 2 6. a 3 a 2 2

Zatem objętość wynosi

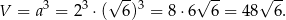
3 3 √ --3 √ -- √ -- V = a = 2 ⋅( 6) = 8 ⋅6 6 = 48 6.

 
Odpowiedź: √ -- 48 6 cm 3

Wersja PDF