/Szkoła średnia/Geometria

Zadanie nr 1044627

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 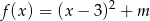f(x) = (x − 3)2 + m , gdzie 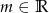m ∈ R – parametr.

Rozwiązanie

Korzystamy z faktu, że jeżeli parabola jest dana w postaci kanonicznej

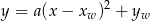
2 y = a(x − xw ) + yw

to 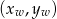(xw ,yw ) są współrzędnymi wierzchołka tej paraboli.

W naszej sytuacji wierzchołek paraboli to

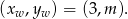
(xw ,yw) = (3,m ).

Punkty te tworzą prostą 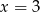x = 3 .  
Odpowiedź: Prosta x = 3

Wersja PDF