/Szkoła średnia/Geometria

Zadanie nr 1152582

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ostrosłup prawidłowy czworokątny o krawędzi bocznej dwa razy dłuższej od krawędzi podstawy.

  • Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa.

  • Wyznacz długość krawędzi ostrosłupa, tak aby pole jego powierzchni bocznej wynosiło √ --- 36 1 5 .

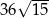Rozwiązanie

Zaczynamy od rysunku

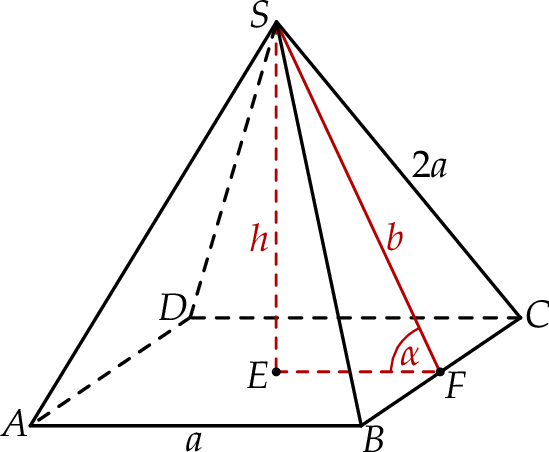
ZINFO-FIGURE

Z twierdzenia Pitagorasa w trójkącie SFC wyznaczamy wysokość ściany bocznej

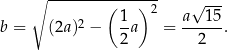
∘ ---------------- ( ) 2 √ --- b = (2a)2 − 1a = a---15. 2 2

  • Obliczamy cosinus kąta nachylenia ściany bocznej

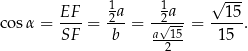
    1a 1a √ --- cosα = EF- = 2--= -2√---= --15. SF b a-15- 15 2

     
    Odpowiedź: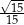 √-- -1155-

  • Liczymy

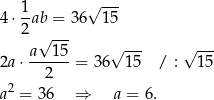
    √ --- 4 ⋅ 1-ab = 36 15 2 √ --- a 1 5 √ --- √ --- 2a ⋅------ = 36 1 5 / : 1 5 2 2 a = 3 6 ⇒ a = 6.

    Krawędzie muszą mieć długość 6 i 12 jednostek.  
    Odpowiedź: 6 i 12 jednostek

Wersja PDF