/Szkoła średnia/Geometria

Zadanie nr 1199631

Dodaj do ulubionych
Dodaj do rozwiązanych

W okręgu o promieniu 5 poprowadzono dwie równoległe cięciwy o długościach 6 i 8. Oblicz odległość między tymi cięciwami.

Rozwiązanie

Zaczynamy od rysunku.

PIC

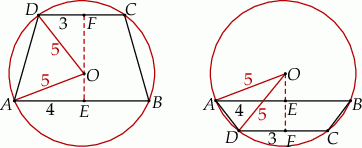
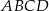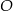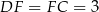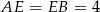Widać, że mamy dwie możliwości poprowadzenia tych cięciw – środek okręgu może być po między nimi albo nie. Zajmijmy się na początek pierwszą sytuacją. Czworokąt ABCD jest trapezem równoramiennym i gdy zrzutujemy środek O okręgu na jego podstawy to mamy DF = FC = 3 oraz AE = EB = 4 . Zatem

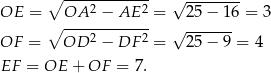
∘ ----2------2 √ -------- OE = OA---−-AE---= 25 − 16 = 3 ∘ 2 2 √ ------- OF = OD − DF = 25 − 9 = 4 EF = OE + OF = 7.

W drugiej sytuacji jest bardzo podobnie

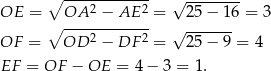
∘ ------------ √ -------- OE = OA 2 − AE 2 = 25 − 16 = 3 ∘ ------------ √ ------- OF = OD 2 − DF 2 = 25 − 9 = 4 EF = OF − OE = 4− 3 = 1.

 
Odpowiedź: 7 lub 1

Wersja PDF