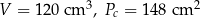Zadanie nr 1224401
Oblicz objętość i pole powierzchni graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze 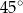 .
.
Rozwiązanie
Zaczynamy od rysunku.
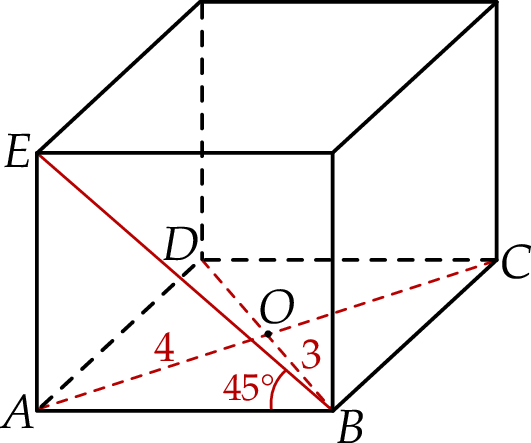
Ponieważ przekątne rombu są prostopadłe i dzielą się na połowy, jego bok jest równy
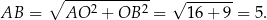
Trójkąt 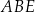 jest prostokątny i jeden z jego kątów jest równy
jest prostokątny i jeden z jego kątów jest równy 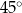 , zatem jest równoramienny. Czyli
, zatem jest równoramienny. Czyli 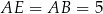 . Zatem objętość graniastosłupa jest równa (korzystamy ze wzoru na pole rombu).
. Zatem objętość graniastosłupa jest równa (korzystamy ze wzoru na pole rombu).
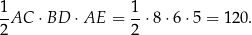
Obliczmy jeszcze pole powierzchni całkowitej.
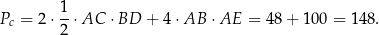
Odpowiedź: