/Szkoła średnia/Geometria

Zadanie nr 1341317

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź zbiór środków wszystkich okręgów stycznych wewnętrznie do okręgu o równaniu 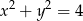x2 + y2 = 4 i stycznych do prostej o równaniu y = 0 .

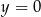Rozwiązanie

Jeżeli punkt 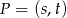P = (s,t) spełnia podane warunki, to jego odległość od prostej 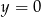y = 0 , czyli 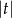|t| , ma być równa jego odległości od danego okręgu.

PIC

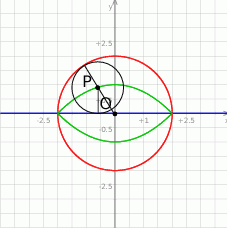
Odległość 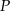P od okręgu to różnica między promieniem okręgu a odległością 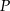P od środka okręgu. Jest ona zatem równa

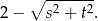
∘ ------- 2 − s2 + t2.

Mamy zatem

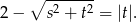
∘ ------- 2− s2 + t2 = |t|.

W zależności od znaku 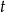t , daje to nam dwa równania

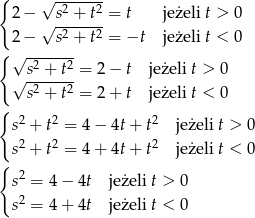
{ √ ------- 2 − s2 + t2 = t jeżeli t > 0 √ -2----2 2 − s + t = −t jeżeli t < 0 { √ -2----2 √ s--+-t-= 2 − t jeżeli t > 0 s2 + t2 = 2 + t jeżeli t < 0 { s2 + t2 = 4 − 4t+ t2 jeżeli t > 0 s2 + t2 = 4 + 4t+ t2 jeżeli t < 0 { s2 = 4 − 4t jeżeli t > 0 2 s = 4 + 4t jeżeli t < 0

Na koniec zauważmy, że aby punkt 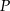P był wewnątrz podanego okręgu, otrzymane krzywe należy obciąć do przedziału s ∈ (− 2,2) .  
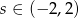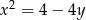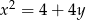Odpowiedź: x2 = 4 − 4y lub x 2 = 4+ 4y dla x ∈ (− 2,2 )

Wersja PDF