/Szkoła średnia/Geometria

Zadanie nr 1341922

Dodaj do ulubionych
Dodaj do rozwiązanych

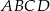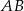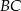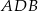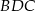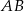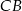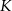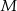W prostokącie ABCD , w którym stosunek długości boków AB i BC jest równy 4:3, poprowadzono dwusieczne kątów ADB i BDC . Dwusieczne te przecinają boki AB i CB odpowiednio w punktach K i M . Oblicz stosunek pola prostokąta 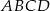ABCD do pola trójkąta DKM .

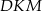Rozwiązanie

Narysujmy opisaną sytuację.

PIC

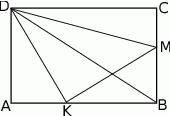
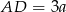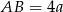Musimy jakoś oznaczyć boki prostokąta, żeby uniknąć ułamków najlepiej oznaczyć AD = 3a i AB = 4a (tak naprawdę możemy nawet wziąć 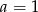a = 1 , bo wielkość prostokąta nie odgrywa w tym zadaniu żadnej roli). Wyliczmy długość przekątnej

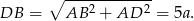
∘ ---2------2- DB = AB + AD = 5a .

Sposób I

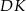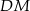Ponieważ proste DK i DM są dwusiecznymi odpowiednich kątów,

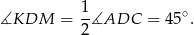
1- ∘ ∡KDM = 2∡ADC = 45 .

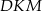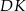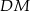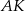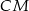Pole trójkąta DKM wyliczymy więc bez trudu ze wzoru z sinusem, o ile tylko będziemy znali długości odcinków DK i DM . Aby je wyliczyć musimy wyliczyć odcinki AK i CM . Robimy to z twierdzenia o dwusiecznej

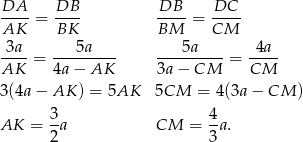
DA DB DB DC ---- = ---- ----= ---- AK BK BM CM -3a- = ----5a--- ---5a----= -4a- AK 4a − AK 3a− CM CM 3(4a − AK ) = 5AK 5CM = 4(3a− CM ) AK = 3a CM = 4a. 2 3

Stąd

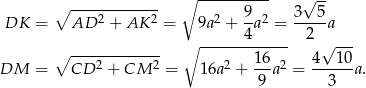
------------ ∘ ---------- √ -- ∘ 2 2 2 9- 2 3--5- DK = AD + AK = 9a + 4 a = 2 a ∘ ------------- ∘ ------------ √ --- DM = CD 2 + CM 2 = 16a 2 + 16a2 = 4--10a. 9 3

Liczymy szukany iloraz pól

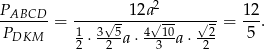
2 PABCD--= ----√---12a√------√--= 12-. PDKM 1 ⋅ 3-5a⋅ 4-10a⋅ -2- 5 2 2 3 2

Sposób II

Tym razem zamiast liczyć pole trójkąta 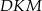DKM policzymy jakie jest pole pozostałej części prostokąta, składającej się z trzech trójkątów prostokątnych.

Podobnie jak poprzednio, z twierdzenia o dwusiecznej wyliczamy, że

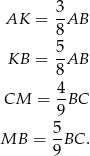
AK = 3-AB 8 5- KB = 8 AB 4 CM = -BC 9 5- MB = 9BC .

Jeżeli przez 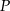P oznaczymy pole prostokąta, to z tych równości wynika, że

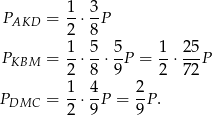
1- 3- PAKD = 2 ⋅ 8P 1 5 5 1 2 5 PKBM = -⋅ --⋅-P = --⋅---P 2 8 9 2 7 2 P = 1⋅ 4P = 2P . DMC 2 9 9

Dodając te równości stronami otrzymujemy

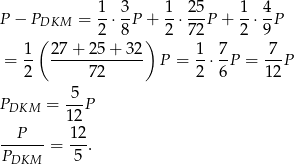
P − PDKM = 1-⋅ 3-P + 1-⋅ 25P + 1⋅ 4P ( 2 8 ) 2 72 2 9 1- 27-+-25-+-32- 1- 7- -7- = 2 72 P = 2 ⋅ 6P = 12 P P = -5P DKM 12 P 1 2 P----- = -5-. DKM

 
Odpowiedź: 12 5

Wersja PDF