/Szkoła średnia/Geometria

Zadanie nr 1353456

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 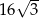√ -- 16 3 , a jego objętość 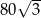√ -- 80 3 . Wyznacz cosinus kąta α nachylenia ściany bocznej do płaszczyzny podstawy.

PIC

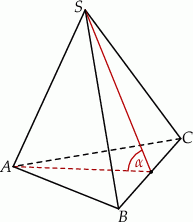
Rozwiązanie

Zaczynamy od rysunku

PIC

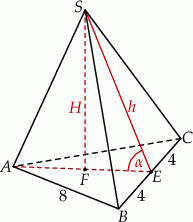
Podane pole podstawy pozwala obliczyć długość boku a trójkąta równobocznego w podstawie ostrosłupa.

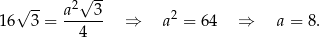
√ -- √ -- a2--3- 2 16 3 = 4 ⇒ a = 64 ⇒ a = 8.

Łatwo też obliczyć wysokość 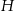H ostrosłupa

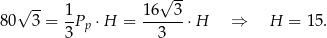
√ -- √ -- 1- 16--3- 8 0 3 = 3 Pp ⋅ H = 3 ⋅H ⇒ H = 15.

Korzystamy teraz z twierdzenia Pitagorasa w trójkącie prostokątnym 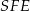SF E i obliczamy wysokość 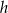h ściany bocznej.

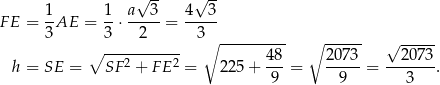
√ -- √ -- 1 1 a 3 4 3 FE = -AE = --⋅-----= ----- 3 3 2 3∘ --------- ∘ ------ √ ----- ∘ ---2-----2- 4-8 2073- --2073- h = SE = SF + FE = 225 + 9 = 9 = 3 .

Pozostało obliczyć cosinus interesującego nas kąta.

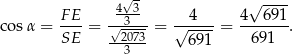
4√3 √ ---- FE- --3--- --4--- 4--691- cosα = SE = √2073 = √ 691 = 69 1 . 3

 
Odpowiedź: √ --- 4-669191

Wersja PDF