Zadanie nr 1676180
Trójkąt równoboczny 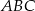 jest podstawą ostrosłupa prawidłowego
jest podstawą ostrosłupa prawidłowego 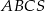 , w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 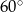 , a krawędź boczna ma długość
, a krawędź boczna ma długość 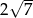 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
(zobacz rysunek). Oblicz objętość tego ostrosłupa.
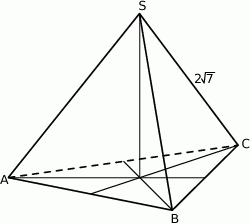
Rozwiązanie
Dorysujmy wysokość 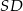 ściany bocznej ostrosłupa.
ściany bocznej ostrosłupa.
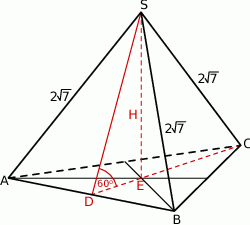
Oznaczmy przez  długość krawędzi podstawy ostrosłupa. Mamy zatem
długość krawędzi podstawy ostrosłupa. Mamy zatem
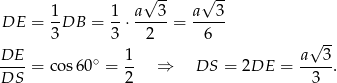
Piszemy teraz twierdzenie Pitagorasa w trójkącie 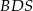 .
.
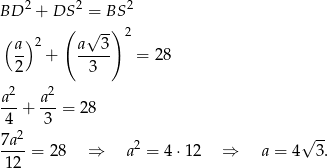
Obliczamy jeszcze wysokość ostrosłupa.
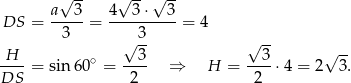
Pozostało obliczyć objętość ostrosłupa.
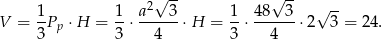
Odpowiedź: