Zadanie nr 3118580
Podstawą ostrosłupa prawidłowego 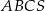 jest trójkąt równoboczny
jest trójkąt równoboczny 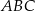 o boku długości 8. Na krawędziach bocznych
o boku długości 8. Na krawędziach bocznych 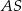 i
i 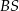 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 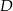 i
i 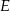 , takie że
, takie że 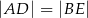 oraz
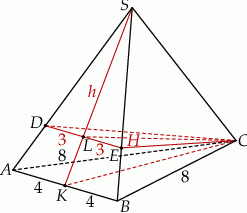
oraz 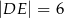 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 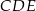 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 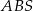 ostrosłupa.
ostrosłupa.
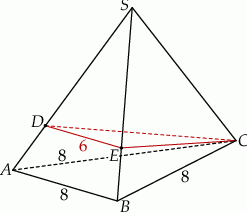
Oblicz objętość tego ostrosłupa.
Rozwiązanie
Jedną z największych trudności tego zadania, to znalezienie sposobu na opisanie prostopadłości płaszczyzn 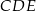 i
i 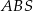 . Aby to zrobić dorysujmy wysokości trójkątów
. Aby to zrobić dorysujmy wysokości trójkątów 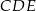 i
i 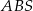 .
.
Prostopadłość płaszczyzn 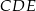 i
i 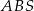 gwarantuje nam teraz prostopadłość wysokości
gwarantuje nam teraz prostopadłość wysokości 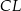 i
i 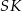 . W szczególności trójkąty
. W szczególności trójkąty 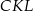 i
i 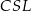 są prostokątne. Jeżeli oznaczymy
są prostokątne. Jeżeli oznaczymy 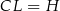 (jest to wysokość czworościanu opuszczona na ścianę
(jest to wysokość czworościanu opuszczona na ścianę 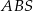 ) i
) i 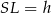 , to
, to
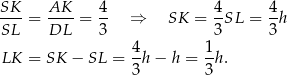
To pozwala nam obliczyć 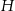 w zależności od
w zależności od 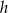 .
.
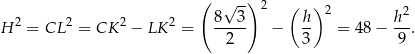
Potrzebujemy jeszcze jednego równania wiążącego te dwie literki – patrzymy na trójkąty prostokątne 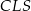 i
i 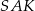 .
.
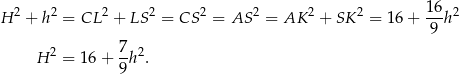
Porównujemy teraz dwa otrzymane wzory na 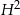 .
.
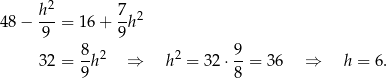
Stąd
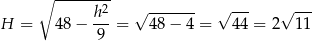
i objętość ostrosłupa jest równa
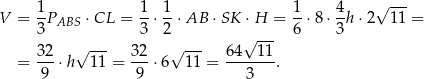
Odpowiedź: