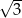/Szkoła średnia/Geometria

Zadanie nr 5238144

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trójkąt prostokątny o polu 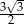3√-3 2 i kącie ostrym 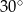∘ 30 . Oblicz długości przyprostokątnych tego trójkąta.

Rozwiązanie

Zaczynamy od rysunku

PIC

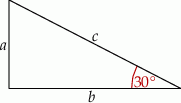
Długości przyprostokątnych możemy wyznaczyć z następującego układu równań

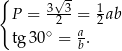
{ √- P = 3-3-= 1ab ∘2 a 2 tg 30 = b.

Z pierwszego równania mamy

√ -- a = 3--3. b

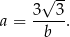
Podstawimy do drugiego równania

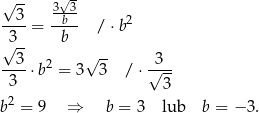
√ -- √ - --3- 3-b3 2 3 = b / ⋅b √ -- √ -- --3-⋅b2 = 3 3 / ⋅√3--- 3 3 2 b = 9 ⇒ b = 3 lub b = − 3.

Odrzucamy wynik ujemny i otrzymujemy

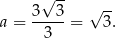
√ -- √ -- a = 3---3 = 3. 3

 
Odpowiedź: 3 i √ -- 3

Wersja PDF