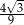/Szkoła średnia/Geometria

Zadanie nr 9000825

Dodaj do ulubionych
Dodaj do rozwiązanych

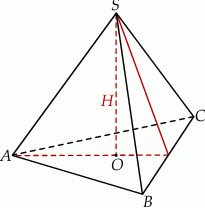
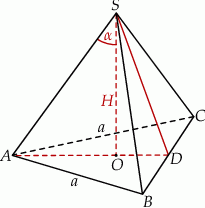
Objętość ostrosłupa prawidłowego trójkątnego 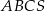ABCS (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie 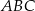ABC tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.

PIC

Rozwiązanie

Dorysujmy wysokość ściany bocznej.

PIC

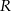Promień R okręgu opisanego na trójkącie równobocznym to 23 wysokości tego trójkąta, więc jeżeli przez a oznaczymy długość krawędzi podstawy to mamy równanie

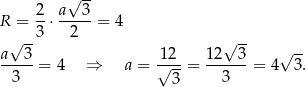
√ -- 2 a 3 R = --⋅-----= 4 √ --3 2 √ -- a--3- 1√2-- 12---3 √ -- 3 = 4 ⇒ a = 3 = 3 = 4 3 .

Możemy teraz wykorzystać informację o objętości ostrosłupa do obliczenia długości jego wysokości

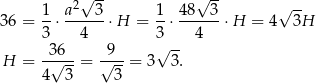
-- -- 1 a2√ 3 1 48√ 3 √ -- 36 = --⋅------⋅H = -⋅ ------⋅H = 4 3H 3 4 3 4 H = -3√6--= √9--= 3√ 3. 4 3 3

Pozostało teraz obliczyć żądany tangens.

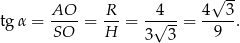
√ -- AO R 4 4 3 tg α = SO--= H- = --√---= --9--. 3 3

 
Odpowiedź: 4√ 3 --9-

Wersja PDF