Zadanie nr 9900597
Średnica 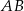 i cięciwa
i cięciwa 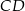 okręgu o środku
okręgu o środku 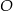 i promieniu
i promieniu  przecinają się w punkcie
przecinają się w punkcie 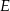 takim, że
takim, że 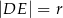 . Wykaż, że
. Wykaż, że 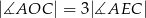 .
.
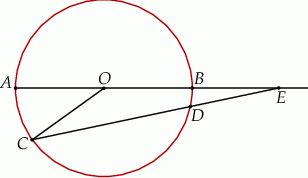
Rozwiązanie
Dorysujmy promień 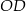 i oznaczmy
i oznaczmy 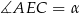 .
.
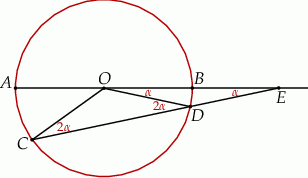
Z założenia trójkąt 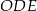 jest równoramienny, więc
jest równoramienny, więc
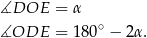
Trójkąt 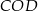 również jest równoramienny, więc
również jest równoramienny, więc
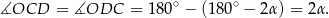
Stąd