/Szkoła średnia/Geometria

Zadanie nr 9963310

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest graniastosłup prawidłowy czworokątny, którego suma długości wszystkich krawędzi wynosi 12.

  • Napisz wzór funkcji 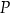P wyrażającej pole powierzchni całkowitej graniastosłupa, w zależności od długości krawędzi podstawy x . Podaj dziedzinę funkcji P .

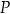  • Wyznacz długości krawędzi graniastosłupa, dla których pole powierzchni całkowitej jest największe.

Rozwiązanie

Zaczynamy od rysunku

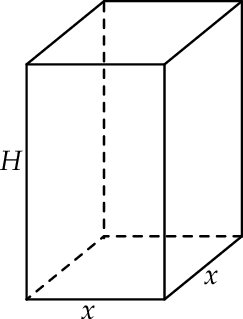
ZINFO-FIGURE

Z warunku na sumę długości wszystkich krawędzi otrzymujemy

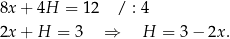
8x + 4H = 12 / : 4 2x + H = 3 ⇒ H = 3 − 2x.

  • Liczymy pole powierzchni całkowitej

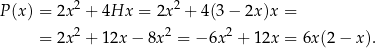
    P (x) = 2x2 + 4Hx = 2x2 + 4(3 − 2x)x = 2 2 2 = 2x + 12x − 8x = − 6x + 12x = 6x(2 − x).

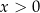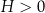    Oczywiście musi być x > 0 oraz H > 0 . Drugą z tych nierówności możemy zapisać w postaci: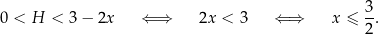

    3- 0 < H < 3 − 2x ⇐ ⇒ 2x < 3 ⇐ ⇒ x ≤ 2.

    Zatem dziedziną jest zbiór ( 3) 0,2 .  
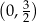    Odpowiedź: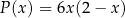 P (x) = 6x (2− x) , dziedzina: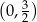 ( ) 0 , 32

  • Musimy znaleźć największą wartość funkcji 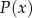P(x ) . Jest to trójmian kwadratowy o ujemnym współczynniku przy najwyższej potędze, więc jego wykresem jest parabola o ramionach skierowanych w dół. Największą wartość pola otrzymamy zatem w wierzchołku, czyli dokładnie w środku między pierwiastkami. Pierwiastkami funkcji 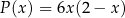P(x ) = 6x(2 − x) są liczby 0 i 2, więc największą wartość pola otrzymamy dla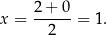

    x = 2-+-0-= 1. 2

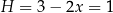    Wtedy H = 3 − 2x = 1 .  
    Odpowiedź: H = x = 1

Wersja PDF