/Szkoła średnia/Geometria

Zadanie nr 9988359

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapezie równoramiennym krótsza podstawa i ramię mają taką samą długość. Przekątna trapezu tworzy z jednym z ramion kąt prosty. Oblicz miary kątów tego trapezu.

Rozwiązanie

Oznaczmy 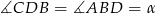∡CDB = ∡ABD = α .

PIC

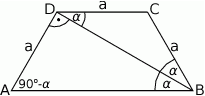
Z założenia wiemy, że trójkąt 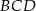BCD jest równoramienny, więc

∡DBC = α.

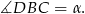
Wiemy też, że trójkąt 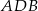ADB jest prostokątny, więc

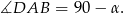
∡DAB = 90− α.

Porównujemy teraz miary kątów trapezu przy wierzchołkach 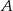A i B .

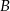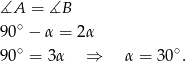
∡A = ∡B 90 ∘ − α = 2α ∘ ∘ 90 = 3α ⇒ α = 30 .

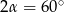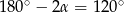To oznacza, że kąty trapezu są równe ∘ 2α = 60 i ∘ ∘ 18 0 − 2α = 120 .  
Odpowiedź: 12 0∘,120∘,60∘,6 0∘

Wersja PDF