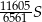Zadanie nr 9996658
Niech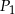 
będzie prostokątem o polu 
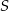i stosunku długości boków równym 3:2. Konstruujemy kolejno prostokąty 
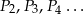podobne do prostokąta 
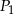takie, że dłuższy bok kolejnego prostokąta jest równy krótszemu bokowi poprzedniego prostokąta. Oblicz sumę pól prostokątów 
.
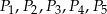Rozwiązanie
Szkicujemy opisaną sytuację.
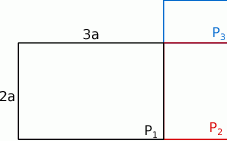
Jeżeli oznaczymy przez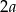 
i 
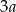boki jednego z prostokątów, to kolejny prostokąt ma boki długości 
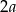oraz
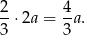
Stosunek pól dwóch kolejnych prostokątów jest więc równy
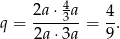
To oznacza, że pola prostokątów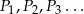 
tworzą ciąg geometryczny 
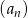o pierwszym wyrazie 
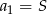i ilorazie 
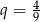. Suma 5 początkowych wyrazów tego ciągu, to
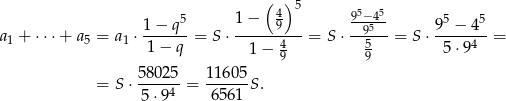
Odpowiedź: 
