/Szkoła średnia/Kombinatoryka/Szuflady, pudełka, urny

Zadanie nr 4075954

Z urny, w której jest 18 losów, w tym 6 wygrywających, wyciągamy 3 losy. Na ile sposobów można wylosować?

  • same losy wygrywające?
  • dokładnie 1 los wygrywający?
  • co najmniej 2 losy wygrywające?
Wersja PDF

Rozwiązanie

  • Pytanie brzmi na ile sposobów można z 6 losów wybrać 3. Możliwości jest
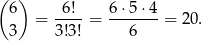
    ( ) 6 6 ! 6⋅ 5⋅4 3 = 3-!3! = ---6---= 20.

     
    Odpowiedź: 20

  • Los wygrywający możemy wybrać na 6 sposobów. Do niego musimy dobrać 2 losy przegrywające, można to zrobić na
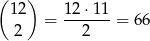
    ( ) 12 = 12-⋅11-= 66 2 2

    sposobów. W sumie daje nam to

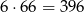
    6⋅6 6 = 396

    sposobów.  
    Odpowiedź: 396

  • Z pierwszego podpunktu wiemy, że trzy losy wygrywające można wybrać na 20 sposobów. Obliczmy jeszcze, na ile sposobów można wybrać dokładnie 2 losy wygrywające.
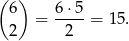
    ( ) 6 = 6-⋅5 = 15. 2 2

    Do tych dwóch losów trzeba dobrać jeden przegrywający, co daje nam

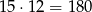
    15 ⋅12 = 180

    układów z 2 losami wygrywającymi. W sumie mamy więc

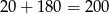
    20 + 180 = 200

    możliwości.  
    Odpowiedź: 200

Wersja PDF