Zadanie nr 6197142
Pięć ponumerowanych kul rozmieszczamy losowo w czterech ponumerowanych szufladach. Oblicz ile jest możliwości takiego rozmieszczenia kul, aby dokładnie dwie szuflady były puste.
Rozwiązanie
Jeżeli dwie szuflady mają być puste, to wszystkie kule muszą trafić do dwóch pozostałych szuflad. Szuflady te możemy wybrać na
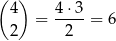
sposobów. Jeżeli już mamy ustalone te dwie szuflady, to kule w pierwszej z nich możemy umieścić na
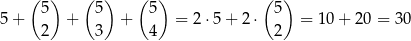
sposobów (możemy tam umieścić jedną, dwie, trzy lub 4 kule). W drugiej z szuflad umieszczamy wszystkie pozostałe kule. W sumie jest więc
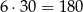
możliwości umieszczenia kul.
Odpowiedź: 180

