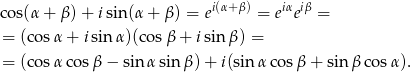Zadanie nr 6783108
Udowodnij, że dla dowolnych kątów 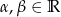 prawdziwe są tożsamości
prawdziwe są tożsamości
Rozwiązanie
Na mocy okresowości funkcji sinus i cosinus, możemy założyć, że  . Zauważmy ponadto, że dodanie
. Zauważmy ponadto, że dodanie 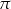 do kąta
do kąta  powoduje zmianę znaków wszystkich wypisanych wyżej funkcji, które w argumencie mają
powoduje zmianę znaków wszystkich wypisanych wyżej funkcji, które w argumencie mają  , na przeciwny. Podobnie jest przy zamianie
, na przeciwny. Podobnie jest przy zamianie  na
na 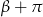 . Oznacza to, że wystarczy dowieść tych wzorów dla
. Oznacza to, że wystarczy dowieść tych wzorów dla  .
.
Podobnie sprawdzamy, co się dzieje, gdy zamienimy  na
na 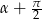 . Po takiej zamianie, pierwszy wzór zamieni się w drugi, a drugi w pierwszy. Analogicznie jest przy zamianie
. Po takiej zamianie, pierwszy wzór zamieni się w drugi, a drugi w pierwszy. Analogicznie jest przy zamianie 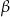 na
na 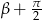 . W ten sposób widzimy, że tak naprawdę wystarczy zajmować się kątami
. W ten sposób widzimy, że tak naprawdę wystarczy zajmować się kątami 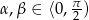 . W dodatku sytuacje
. W dodatku sytuacje 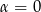 lub
lub  możemy sprawdzić bezpośrednio, więc zostaje nam przedział
możemy sprawdzić bezpośrednio, więc zostaje nam przedział 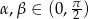 .
.
Sposób I
Skorzystamy z twierdzenia sinusów.
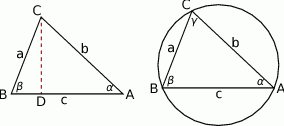
Zauważmy najpierw, że przy oznaczeniach z rysunku, mamy
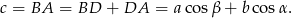
Patrzymy teraz na prawy obrazek, w którym wpisaliśmy trójkąt 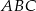 w okrąg o średnicy 1. Na mocy twierdzenia sinusów mamy
w okrąg o średnicy 1. Na mocy twierdzenia sinusów mamy
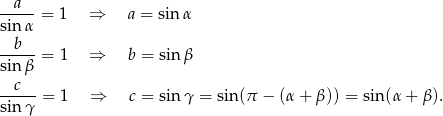
W połączeniu z poprzednią równością daje nam to
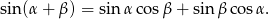
W podobny sposób uzasadniamy wzór na sinus różnicy. Tym razem bierzemy trójkąt o kątach  i
i  .
.
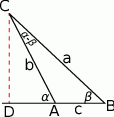
Podobnie jak poprzednio mamy
Jeżeli założymy, że okrąg opisany na tym trójkącie ma średnicę 1, to jak poprzednio, z twierdzenia sinusów mamy
W sumie dostajemy więc
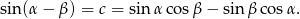
Jeżeli teraz podstawimy w tym wzorze 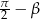 zamiast
zamiast 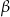 i skorzystamy ze wzorów redukcyjnych, otrzymamy wzór na cosinus sumy.
i skorzystamy ze wzorów redukcyjnych, otrzymamy wzór na cosinus sumy.
Sposób II
Tym razem założymy dodatkowo, że  (tak naprawdę robimy to tylko po to, żeby nie rysować dwóch rysunków w zależności od tego, czy
(tak naprawdę robimy to tylko po to, żeby nie rysować dwóch rysunków w zależności od tego, czy 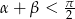 czy nie). Jeżeli tak nie jest, to można zamienić
czy nie). Jeżeli tak nie jest, to można zamienić  na
na 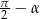 oraz
oraz 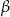 na
na 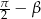 i skorzystać ze wzorów redukcyjnych.
i skorzystać ze wzorów redukcyjnych.
Przyjmijmy oznaczenia z obrazka.
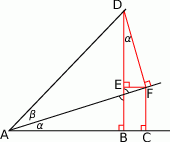
Liczymy
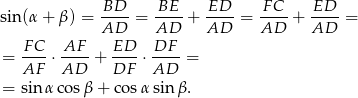
Podobnie

Sposób III
Tym razem użyjemy rachunku wektorowego. Zacznijmy od narysowania w układzie współrzędnych wektora jednostkowego 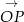 o początku w punkcie
o początku w punkcie 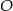 i tworzącego z osią
i tworzącego z osią 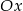 kąt
kąt  .
.
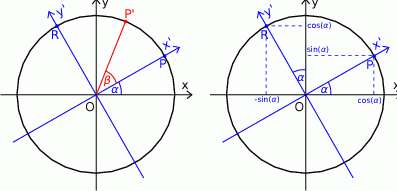
Wtedy  . Niech
. Niech  będzie wektorem, który powstaje z
będzie wektorem, który powstaje z  przez obrót względem punktu
przez obrót względem punktu 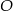 o kąt
o kąt 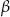 . Oczywiście
. Oczywiście
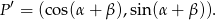
Spróbujemy teraz wyliczyć współrzędne punktu 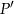 w inny sposób.
w inny sposób.
Niech 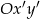 będzie układem współrzędnych, który powstaje z
będzie układem współrzędnych, który powstaje z 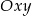 przez obrót względem punktu
przez obrót względem punktu 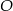 o kąt
o kąt  . W szczególności oś
. W szczególności oś 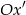 jest wyznaczona przez wektor
jest wyznaczona przez wektor ![→ OP = [cosα,sin α]](https://img.zadania.info/zad/6783108/HzadR54x.gif) . W takim razie druga oś jest wyznaczona przez wektor
. W takim razie druga oś jest wyznaczona przez wektor 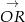 , który jest prostopadły do
, który jest prostopadły do  . Łatwo odgadnąć współrzędne tego wektora:
. Łatwo odgadnąć współrzędne tego wektora: ![→ OR = [− sin α,co sα]](https://img.zadania.info/zad/6783108/HzadR57x.gif) (prawy obrazek).
(prawy obrazek).
W układzie współrzędnych 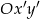 wektor
wektor  ma współrzędne
ma współrzędne ![[cos β,sinβ ]](https://img.zadania.info/zad/6783108/HzadR60x.gif) , co nam daje następujące współrzędne w układzie
, co nam daje następujące współrzędne w układzie 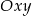 .
.
![→ → → OP ′ = cos β⋅OP + sin β ⋅OR = co sβ ⋅[cosα ,sin α]+ sin β ⋅[− sinα ,cosα] = = [cosβ cos α− sin β sin α,co sβ sin α + sinβ cos α].](https://img.zadania.info/zad/6783108/HzadR62x.gif)
W połączeniu z wcześniej zauważoną równością
![→ OP ′ = [cos(α+ β),sin(α + β)]](https://img.zadania.info/zad/6783108/HzadR63x.gif)
daje to nam żądane równości.
Sposób IV
Podobnie jak poprzednio, użyjemy geometrii analitycznej. Tym razem załóżmy, że  i narysujmy w układzie współrzędnych wektory jednostkowe
i narysujmy w układzie współrzędnych wektory jednostkowe 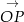 i
i  , które tworzą z osią
, które tworzą z osią  odpowiednio kąty
odpowiednio kąty  i
i  .
.

Wyliczymy długość odcinka  na dwa sposoby.
na dwa sposoby.
Jeżeli dorysujemy trójkąt prostokątny  , o bokach równoległych do osi układu, to mamy
, o bokach równoległych do osi układu, to mamy
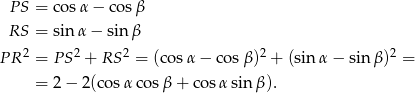
Jeżeli natomiast zrzutujemy punkt 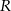 na prostą
na prostą 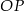 , to mamy trójkąt prostokątny
, to mamy trójkąt prostokątny 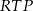 , w którym
, w którym
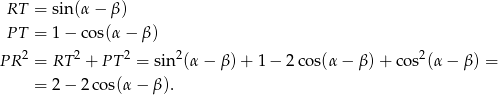
Porównując dwa otrzymane wzory na 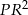 mamy
mamy
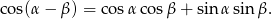
Aby otrzymać wzór na sinus sumy, podstawiamy w otrzymanym wzorze 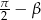 zamiast
zamiast 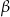 .
.
Pozostało wyprowadzić wzór na cosinus sumy. Jak już zauważyliśmy w Sposobie I, wystarczy wyprowadzić wzór na sinus różnicy. Możemy założyć, że 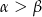 i korzystamy z jedynki trygonometrycznej
i korzystamy z jedynki trygonometrycznej
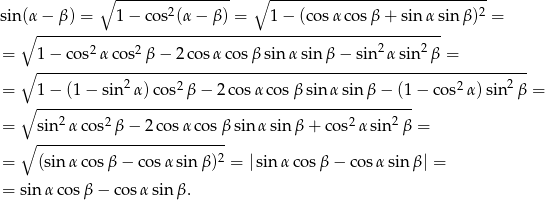
Wartość bezwzględną opuściliśmy korzystając z tego, że sinus jest rosnący, cosinus malejący dla kątów ostrych, więc wyrażenie pod wartością bezwzględną jest dodatnie.
Sposób V
Ten sposób będzie bardzo podobny do Sposobu I, ale obejdziemy się bez twierdzenia sinusów. Tak jak w Sposobie II, zakładamy, że 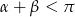 . Rysujemy trójkąt o kątach
. Rysujemy trójkąt o kątach 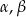 i jego wysokości
i jego wysokości 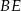 i
i 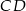 (lewy rysunek).
(lewy rysunek).

Jeżeli przyjmiemy 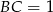 , to mamy
, to mamy

Teraz wystarczy popatrzeć na trójkąt  .
.
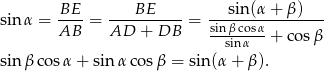
Wzór na sumę cosinusów wyprowadzamy parząc na prawy rysunek. Jeżeli przyjmiemy 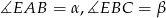 oraz
oraz  , to jest jasne, że
, to jest jasne, że
Patrzymy teraz na trójkąt 
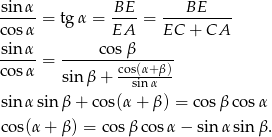
Sposób VI
Wzory na sinus sumy i różnicy są prostym wnioskiem z twierdzeń Ptolemeusza i sinusów.
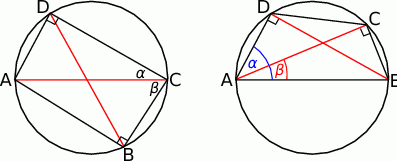
Niech 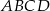 będzie czworokątem wpisanym w okrąg o średnicy
będzie czworokątem wpisanym w okrąg o średnicy 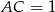 , w którym
, w którym 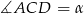 i
i 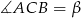 (lewy rysunek). Mamy wtedy
(lewy rysunek). Mamy wtedy

Ponadto, z twierdzenia sinusów mamy
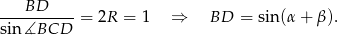
Pozostało teraz napisać twierdzenie Ptolemeusza.
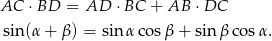
Wzór na sinus różnicy wyprowadzamy z prawego rysunku. Tym razem średnicą okręgu niech będzie 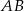 oraz
oraz  . Mamy wtedy
. Mamy wtedy

Ponadto z twierdzenia sinusów mamy
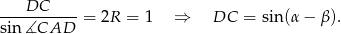
Pozostało teraz napisać twierdzenie Ptolemeusza.
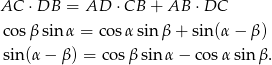
Z tego wzoru wyprowadzamy wzór na cosinus sumy podstawiając 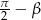 zamiast
zamiast 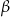 .
.
Sposób VII
Żądane wzory łatwo wyprowadzić, jeżeli użyje się odrobinę algebry liniowej (w zasadzie będzie to inny sposób zapisu Sposobu III).
Obrót płaszczyzny 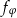 o kąt
o kąt 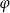 względem początku układu współrzędnych jest odwzorowaniem liniowym – spróbujemy napisać jego macierz. Aby to zrobić, wystarczy sprawdzić jakie są obrazy wektorów bazowych
względem początku układu współrzędnych jest odwzorowaniem liniowym – spróbujemy napisać jego macierz. Aby to zrobić, wystarczy sprawdzić jakie są obrazy wektorów bazowych ![[1,0]](https://img.zadania.info/zad/6783108/HzadR115x.gif) i
i ![[0,1]](https://img.zadania.info/zad/6783108/HzadR116x.gif) .
.
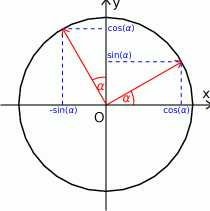
Gdy się popatrzy na obrazek, to widać, że
![fφ ([1,0 ]) = [cos φ,sin φ] fφ ([0,1 ]) = [− sin φ,cos φ].](https://img.zadania.info/zad/6783108/HzadR118x.gif)
Zatem macierz odwzorowania 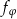 ma postać
ma postać
![[ ] co sφ − sin φ M (fφ ) = sin φ cosφ .](https://img.zadania.info/zad/6783108/HzadR120x.gif)
Teraz pozostało skorzystać z oczywistej równości
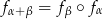
(obrót płaszczyzny najpierw o  , a potem o
, a potem o 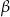 to to samo, co obrót o
to to samo, co obrót o 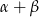 ). Daje nam to
). Daje nam to
![[ ] [ ] [ ] cos(α+ β) − sin(α + β ) = cosβ − sinβ ⋅ cos α − sin α sin (α+ β) cos(α + β ) sinβ cosβ sin α cosα.](https://img.zadania.info/zad/6783108/HzadR125x.gif)
Wymnażając macierze z prawej strony, otrzymamy żądane wzory.
Sposób VIII
Osoby, którym nie są obce liczby zespolone, mogą rozwiązanie ze Sposobu III zapisać w bardzo eleganckiej formie