/Szkoła średnia/Kombinatoryka/Geometryczne

Zadanie nr 3732355

Dodaj do ulubionych
Dodaj do rozwiązanych

Na jednej prostej zaznaczono 3 punkty, a na drugiej 4 punkty.

PIC

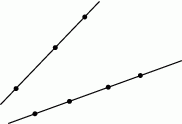
Ile jest wszystkich trójkątów, których wierzchołkami są trzy spośród zaznaczonych punktów?

Rozwiązanie

Sposób I

Trójkąt ma trzy wierzchołki i nie mogą one leżeć na jednej prostej. Jeżeli dwa wierzchołki leżą na prostej z trzema punktami, to można jest wybrać na 3 sposoby (bo na trzy sposoby można wybrać punkt, który nie będzie wierzchołkiem). Do tego na 4 sposoby można wybrać trzeci wierzchołek (na drugiej prostej), co daje nam (zasada mnożenia)

3 ⋅4 = 12

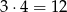
trójkątów.

Jeżeli natomiast dwa wierzchołki są na prostej z 4 punktami, to można je wybrać na

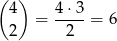
( ) 4 = 4⋅-3 = 6 2 2

sposobów. Do tego na 3 sposoby wybieramy trzeci wierzchołek, co daje

6 ⋅3 = 18

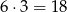
trójkątów.

W sumie jest więc

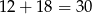
12+ 18 = 30

trójkątów.

Sposób II

Spośród danych punktów możemy wybrać 3 na

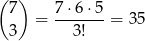
( 7) 7⋅ 6⋅5 = -------= 35 3 3!

sposobów. Nie wszystkie wybrane trójki dają nam jednak trójkąty: jest jedna zła trójka, gdy wybrane punkty leżą na górnej prostej, oraz 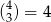(4) = 4 3 złe trójki, gdy wybrane punkty leżą na dolnej prostej. W sumie jest więc

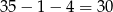
35 − 1 − 4 = 3 0

takich trójkątów.  
Odpowiedź: 30

Wersja PDF