Zadanie nr 6796903
Na okręgu zaznaczono sześć różnych punktów. Ile różnych wielokątów wypukłych o wszystkich wierzchołkach w tych punktach można narysować?
Rozwiązanie
Punktów jest 6, więc w rachubę wchodzą tylko trójkąty, czworokąty, pięciokąty i sześciokąty.
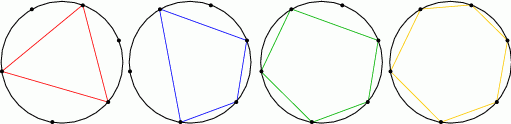
Sześciokąt jest oczywiście jeden, więc tak naprawdę pozostało policzyć trójkąty, czworokąty i pięciokąty.
Trójkątów jest tyle, na ile sposobów spośród 6 punktów można wybrać 3, czyli
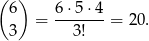
Podobnie jest z czworokątami – ponieważ mają być wypukłe, cztery punkty wyznaczają dokładnie jeden czworokąt (bo musimy łączyć punkty w kolejności w jakiej leżą na okręgu). Jest ich więc
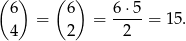
Pięciokątów jest
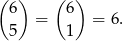
W sumie mamy więc
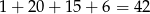
wielokąty.
Odpowiedź: 42

