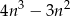Zadanie nr 8727110
Proste 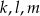 są parami różne i równoległe. Na prostych tych wybrano zbiór
są parami różne i równoległe. Na prostych tych wybrano zbiór 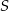 składający się z
składający się z 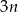 punktów (
punktów (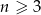 ), przy czym na każdej z prostych wybrano
), przy czym na każdej z prostych wybrano  punktów. Wiadomo ponadto, że jeżeli trzy punkty zbioru
punktów. Wiadomo ponadto, że jeżeli trzy punkty zbioru 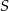 leżą na jednej prostej, to prostą tą jest
leżą na jednej prostej, to prostą tą jest 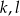 lub
lub 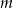 . Oblicz ile jest trójkątów o wierzchołkach należących do zbioru
. Oblicz ile jest trójkątów o wierzchołkach należących do zbioru 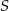 .
.
Rozwiązanie
Sposób I
Mamy dwa rodzaje trójkątów: takie, których dwa wierzchołki leżą na jednej z podanych prostych oraz takie, że każdy wierzchołek leży na innej prostej.
Łatwo policzyć trójkąty drugiego rodzaju – wiemy, że jeżeli wybierzemy po jednym punkcie z każdej prostej, to punkty te nie będą współliniowe, czyli będą tworzyły trójkąt. Jest więc
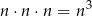
takich trójkątów (wybieramy po jednym punkcie z każdej prostej).
Pozostało policzyć trójkąty pierwszego rodzaju. Na 3 sposoby możemy wybrać prostą, na której będą dwa wierzchołki trójkąta. Jeżeli prosta jest już ustalona, to dwa wierzchołki możemy wybrać na
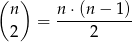
sposobów. Trzeci wierzchołek wybieramy zupełnie dowolnie spośród 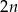 punktów z dwóch pozostałych prostych. W sumie jest więc
punktów z dwóch pozostałych prostych. W sumie jest więc
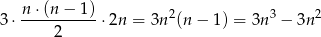
trójkątów pierwszego rodzaju.
Razem jest więc
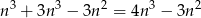
trójkątów.
Sposób II
Trzy punkty spośród 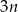 możemy wybrać na
możemy wybrać na
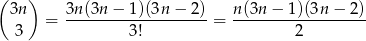
sposobów. To oczywiście nie koniec, bo nie każde trzy punkty tworzą trójkąt. Wiemy jednak, że „złe” trójki to dokładnie trójki punktów z prostych 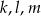 . Jest
. Jest
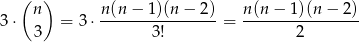
takich trójek (wybieramy jedną z prostych i trzy jej punkty).
Jest zatem
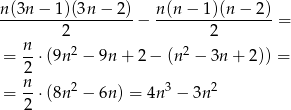
„dobrych” trójkątów.
Odpowiedź: