Zadanie nr 4034221
Rozwiązaniem nierówności 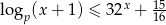 z niewiadomą
z niewiadomą  jest zbiór
jest zbiór 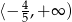 . Wyznacz
. Wyznacz 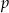 .
.
Rozwiązanie
Myślimy o wykresach obu stron. Wykres prawej strony jesteśmy w stanie dość dokładnie naszkicować – jest to wykres funkcji 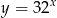 przesunięty o
przesunięty o 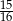 do góry.
do góry.
Zastanówmy się teraz jak może wyglądać wykres lewej strony. Jest to oczywiście wykres funkcji 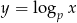 przesunięty o jedną jednostkę w lewo. Gdyby
przesunięty o jedną jednostkę w lewo. Gdyby 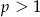 to logarytm dążyłby do
to logarytm dążyłby do 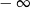 przy
przy  zbliżającym się do -1, a więc na pewno rozwiązaniami podanej nierówności byłyby liczby dowolnie bliskie -1. Takich liczb jednak nie ma w zbiorze rozwiązań, więc musi być
zbliżającym się do -1, a więc na pewno rozwiązaniami podanej nierówności byłyby liczby dowolnie bliskie -1. Takich liczb jednak nie ma w zbiorze rozwiązań, więc musi być 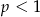 . Teraz możemy naszkicować oba wykresy.
. Teraz możemy naszkicować oba wykresy.
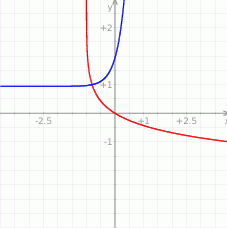
Widać teraz, że wykres funkcji 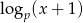 jest poniżej wykresu funkcji
jest poniżej wykresu funkcji 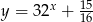 dokładnie na prawo od punktu przecięcia się tych wykresów. Z drugiej strony wiemy, że zbiorem rozwiązań jest przedział
dokładnie na prawo od punktu przecięcia się tych wykresów. Z drugiej strony wiemy, że zbiorem rozwiązań jest przedział 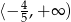 . To oznacza, że wykresy muszą się przecinać dla
. To oznacza, że wykresy muszą się przecinać dla 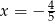 . Sprawdźmy jaka jest wtedy wartość funkcji
. Sprawdźmy jaka jest wtedy wartość funkcji 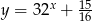 .
.
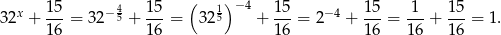
W takim razie dokładnie taką samą wartość w tym punkcie musi przyjmować funkcja 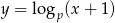 . Wiemy jednak, że
. Wiemy jednak, że 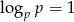 , więc musimy mieć
, więc musimy mieć
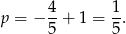
Odpowiedź: