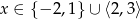/Szkoła średnia/Nierówności/Inne

Zadanie nr 8065648

Rozwiąż nierówność

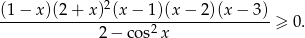
2 (1-−-x)(2-+-x-)(x-−-1-)(x−--2)(x−--3) ≥ 0. 2− cos2x
Wersja PDF

Rozwiązanie

Przekształćmy podaną nierówność

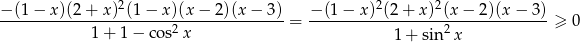
2 2 2 −-(1-−-x)(2-+-x)-(1-−-x)(x-−-2-)(x−--3) = −-(1-−-x)-(2-+-x-)-(x-−--2)(x−--3) ≥ 0 1+ 1 − co s2x 1+ sin 2x

Ponieważ 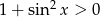1 + sin2 x > 0 , to nierówność ta jest równoważna nierówności

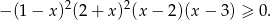
− (1 − x)2(2 + x )2(x − 2 )(x− 3) ≥ 0.

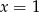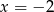Pierwsze dwa nawiasy są zawsze nieujemne, więc pamiętając o dołożeniu na koniec liczb x = 1 i x = − 2 do zbioru rozwiązań, pozostaje nam nierówność

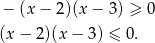
− (x − 2)(x − 3) ≥ 0 (x − 2)(x − 3 ) ≤ 0.

Jest to zwykła nierówność kwadratowa, której rozwiązaniem jest przedział 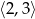⟨2,3⟩ .  
Odpowiedź: x ∈ { − 2,1} ∪ ⟨2,3⟩

Wersja PDF