/Szkoła średnia/Zadania maturalne/Matura 2007

Egzamin Maturalny
z Matematyki poziom rozszerzony 14 maja 2007 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

Dana jest funkcja 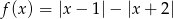f (x) = |x− 1|− |x + 2| dla x ∈ R .

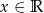  • Wyznacz zbiór wartości funkcji 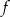f dla x ∈ (− ∞ ,− 2) .
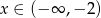  • Naszkicuj wykres tej funkcji.
  • Podaj jej miejsca zerowe.
  • Wyznacz wszystkie wartości parametru 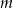m , dla których równanie 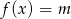f(x) = m nie ma rozwiązania.

Zadanie 2
(5 pkt)

Rozwiąż nierówność:

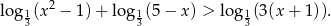
log 1(x2 − 1)+ lo g1(5 − x) > log 1(3(x + 1)). 3 3 3

Zadanie 3
(5 pkt)

Kapsuła lądownika ma kształt stożka zakończonego w podstawie półkulą o tym samym promieniu co promień podstawy stożka. Wysokość stożka jest o 1 m większa niż promień półkuli. Objętość stożka stanowi 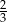2 3 objętości całej kapsuły. Oblicz objętość kapsuły lądownika.

Zadanie 4
(3 pkt)

Dany jest trójkąt o bokach długości 1, 3 2 , 2. Oblicz cosinus i sinus kąta leżącego naprzeciw najkrótszego boku tego trójkąta.

Zadanie 5
(7 pkt)

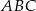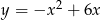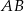Wierzchołki trójkąta równobocznego ABC są punktami paraboli 2 y = −x + 6x . Punkt C jest jej wierzchołkiem, a bok AB jest równoległy do osi 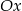Ox . Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.

Zadanie 6
(4 pkt)

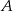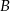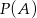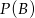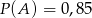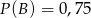Niech A , B będą zdarzeniami o prawdopodobieństwach P (A ) i P(B ) . Wykaż, że jeżeli P (A ) = 0,85 i P (B) = 0,75 , to prawdopodobieństwo warunkowe spełnia nierówność 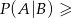P(A |B) ≥ 0,8.

Zadanie 7
(7 pkt)

Dany jest układ równań: 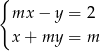{ mx − y = 2 x+ my = m .
Dla każdej wartości parametru 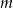m wyznacz parę liczb 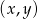(x,y) , która jest rozwiązaniem tego układu równań. Wyznacz najmniejszą wartość sumy 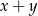x + y dla m ∈ ⟨2,4⟩ .

Zadanie 8
(3 pkt)

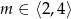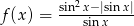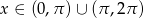Dana jest funkcja f określona wzorem sin2x−|sinx| f(x) = ---sin-x---- dla x ∈ (0,π) ∪ (π ,2π) .

  • Naszkicuj wykres funkcji f .
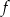  • Wyznacz miejsca zerowe funkcji f .

Zadanie 9
(3 pkt)

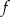Przedstaw wielomian 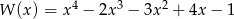W (x) = x4 − 2x3 − 3x2 + 4x − 1 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.

Zadanie 10
(4 pkt)

Na kole opisany jest romb. Stosunek pola koła do pola powierzchni rombu wynosi 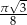√- π-83 . Wyznacz miarę kąta ostrego rombu.

Zadanie 11
(4 pkt)

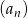Suma n początkowych wyrazów ciągu arytmetycznego (an) wyraża się wzorem 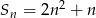Sn = 2n2 + n dla n ≥ 1 .

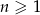  • Oblicz sumę 50 początkowych wyrazów tego ciągu o numerach parzystych:
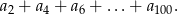
    a2 + a4 + a6 + ...+ a 100.
  • Oblicz
    S lim ----n--- n→+ ∞ 3n2 − 2

Arkusz Wersja PDF
Rozwiązania