/Studia/Podstawy matematyki/Indukcja

Zadanie nr 5265846

Dodaj do ulubionych
Dodaj do rozwiązanych

Stosując zasadę indukcji matematycznej, wykaż, że dla każdej liczby naturalnej dodatniej n zachodzi równość

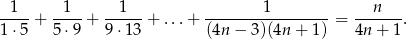
--1- + --1- + --1--+ ...+ --------1-------- = --n---. 1 ⋅5 5 ⋅9 9⋅13 (4n − 3)(4n + 1) 4n + 1

Rozwiązanie

Sprawdzamy dla 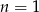n = 1 .

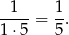
1 1 ---- = -. 1 ⋅5 5

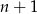Załóżmy teraz, że wzór jest prawdziwy dla liczby naturalnej n i pokażemy jego prawdziwość dla liczby n + 1 . Liczymy lewą stronę dla n + 1 .

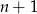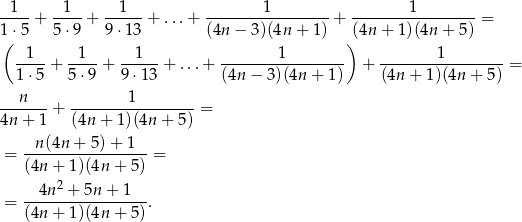
1 1 1 1 1 ---- + ----+ -----+ ...+ ----------------- + ----------------- = 1(⋅5 5⋅9 9⋅1 3 (4n − 3)(4n + 1) )(4n + 1)(4n + 5) --1- -1-- --1--- -------1--------- --------1-------- 1 ⋅5 + 5⋅9 + 9⋅ 13 + ...+ (4n− 3)(4n + 1) + (4n + 1)(4n + 5) = ---n---+ --------1-------- = 4n + 1 (4n + 1)(4n + 5) n(4n + 5)+ 1 = -----------------= (4n+ 1)(4n + 5) 4n2 + 5n + 1 = -----------------. (4n+ 1)(4n + 5)

Aby dalej przekształcić to wyrażenie, musimy rozłożyć licznik na iloczyn. Ponieważ wiemy co ma wyjść, łatwo to zrobić (można oczywiście też to zrobić z Δ -y).

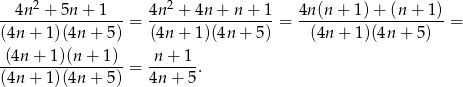
4n 2 + 5n + 1 4n2 + 4n + n + 1 4n (n+ 1)+ (n+ 1) ----------------- = -----------------= -------------------- = (4n + 1)(4n + 5) (4n + 1)(4n + 5 ) (4n + 1)(4n + 5) (4n + 1)(n + 1 ) n + 1 ----------------- = ------. (4n + 1)(4n + 5) 4n + 5

To co otrzymaliśmy to dokładnie prawa strona dla 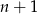n+ 1 .

Wersja PDF