/Szkoła średnia/Zadania maturalne/Matura 2009/Matura próbna/CKE

Próbny Egzamin Maturalny
z Matematyki poziom podstawowy 13 stycznia 2009 Czas pracy: 120 minut

Zadanie 1
(4 pkt)

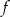Funkcja f jest określona wzorem

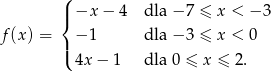
( |{ −x − 4 dla − 7 ≤ x < − 3 f (x) = |( −1 dla − 3 ≤ x < 0 4x− 1 dla 0 ≤ x ≤ 2.
  • Podaj dziedzinę funkcji f .
  • Podaj jej miejsca zerowe.
  • Naszkicuj wykres tej funkcji.
  • Podaj zbiór wartości funkcji f .

Zadanie 2
(3 pkt)

Spośród cyfr 1, 2, 3, 4, 5, 6 losujemy kolejno dwa razy po jednej cyfrze ze zwracaniem. Tworzymy liczbę dwucyfrową w ten sposób, że pierwsza z wylosowanych cyfr jest cyfrą dziesiątek, a druga cyfrą jedności tej liczby. Oblicz prawdopodobieństwo utworzenia liczby większej od 52.

Zadanie 3
(4 pkt)

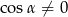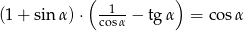Uzasadnij, że jeżeli co sα ⁄= 0 to prawdą jest, że ( ) (1+ sin α) ⋅ -1--− tg α = cosα cosα .

Zadanie 4
(4 pkt)

Liczba 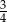3 4 jest pierwszym wyrazem ciągu geometrycznego 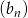(bn) , którego iloraz jest równy 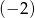(− 2) . Pierwszy wyraz ciągu arytmetycznego 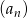(an) jest taki sam jak pierwszy wyraz ciągu 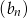(bn) . Suma siedmiu początkowych wyrazów ciągu 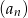(an) jest równa sumie siedmiu początkowych wyrazów ciągu 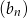(bn) . Oblicz różnicę ciągu arytmetycznego (an) .

Zadanie 5
(6 pkt)

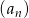Rozwiąż nierówność 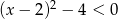(x − 2)2 − 4 < 0 . Podaj wszystkie rozwiązania równania 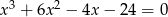3 2 x + 6x − 4x − 24 = 0 , które należą do zbioru rozwiązań tej nierówności.

Zadanie 6
(4 pkt)

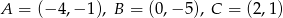Punkty A = (− 4,− 1), B = (0 ,−5 ), C = (2,1) są wierzchołkami trójkąta równoramiennego. Wyznacz równanie osi symetrii tego trójkąta.

Zadanie 7
(5 pkt)

Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem 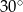30∘ . Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa.

Zadanie 8
(3 pkt)

Dziadek założył w banku trzyletnią lokatę pieniężną o stałej rocznej stopie procentowej równej 5% (już po uwzględnieniu podatków i prowizji). Odsetki są kapitalizowane po każdym roku trwania lokaty. Całość środków, otrzymanych z banku po zlikwidowaniu lokaty, dziadek podzielił równo pomiędzy dziewięcioro wnucząt tak, że każde z dzieci otrzymało 1029 zł. Oblicz początkową kwotę lokaty.

Zadanie 9
(4 pkt)

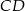W trójkącie ostrokątnym ABC bok AB ma długość 18 cm, a wysokość CD jest równa 15 cm. Punkt 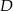D dzieli bok 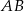AB tak, że 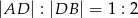|AD | : |DB | = 1 : 2 . Przez punkt 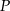P leżący na odcinku 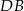DB poprowadzono prostą równoległą do prostej 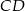CD , odcinając od trójkąta 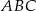ABC trójkąt, którego pole jest cztery razy mniejsze niż pole trójkąta 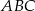ABC . Oblicz długość odcinka P B .

Zadanie 10
(5 pkt)

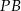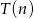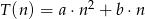Doświadczalnie ustalono, że czas T(n ) , liczony w sekundach, potrzebny na alfabetyczne ułożenie n kartek z nazwiskami wyraża się, z dobrym przybliżeniem, wzorem T (n) = a ⋅n2 + b ⋅n . Ułożenie 10 kartek trwa średnio 20 sekund, a 30 kartek średnio 90 sekund. Wyznacz wzór funkcji 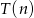T (n) i oblicz, ile kartek można ułożyć średnio w ciągu 50 sekund.

Zadanie 11
(4 pkt)

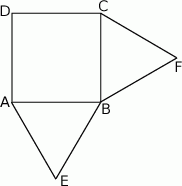
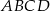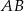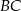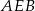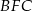Na zewnątrz kwadratu ABCD na bokach AB i BC zbudowano trójkąty równoboczne AEB i BFC . Uzasadnij, że trójkąt 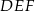DEF jest równoboczny.

PIC

Zadanie 12
(4 pkt)

W pewnej klasie liczba dziewcząt stanowi 60% liczby osób w tej klasie. Gdy 6 dziewcząt wyjechało na mecz siatkówki, w klasie pozostało tyle samo chłopców, ile dziewcząt. Oblicz, ile osób liczy ta klasa oraz ilu jest w niej chłopców.

Arkusz Wersja PDF
Rozwiązania